BOJ_1167_트리의 지름 (Java)

[Gold II] 트리의 지름 - 1167

문제 링크

성능 요약

메모리: 87836 KB, 시간: 764 ms

분류

깊이 우선 탐색, 그래프 이론, 그래프 탐색, 트리

제출 일자

2024년 9월 18일 00:52:01

문제 설명

트리의 지름이란, 트리에서 임의의 두 점 사이의 거리 중 가장 긴 것을 말한다. 트리의 지름을 구하는 프로그램을 작성하시오.

입력

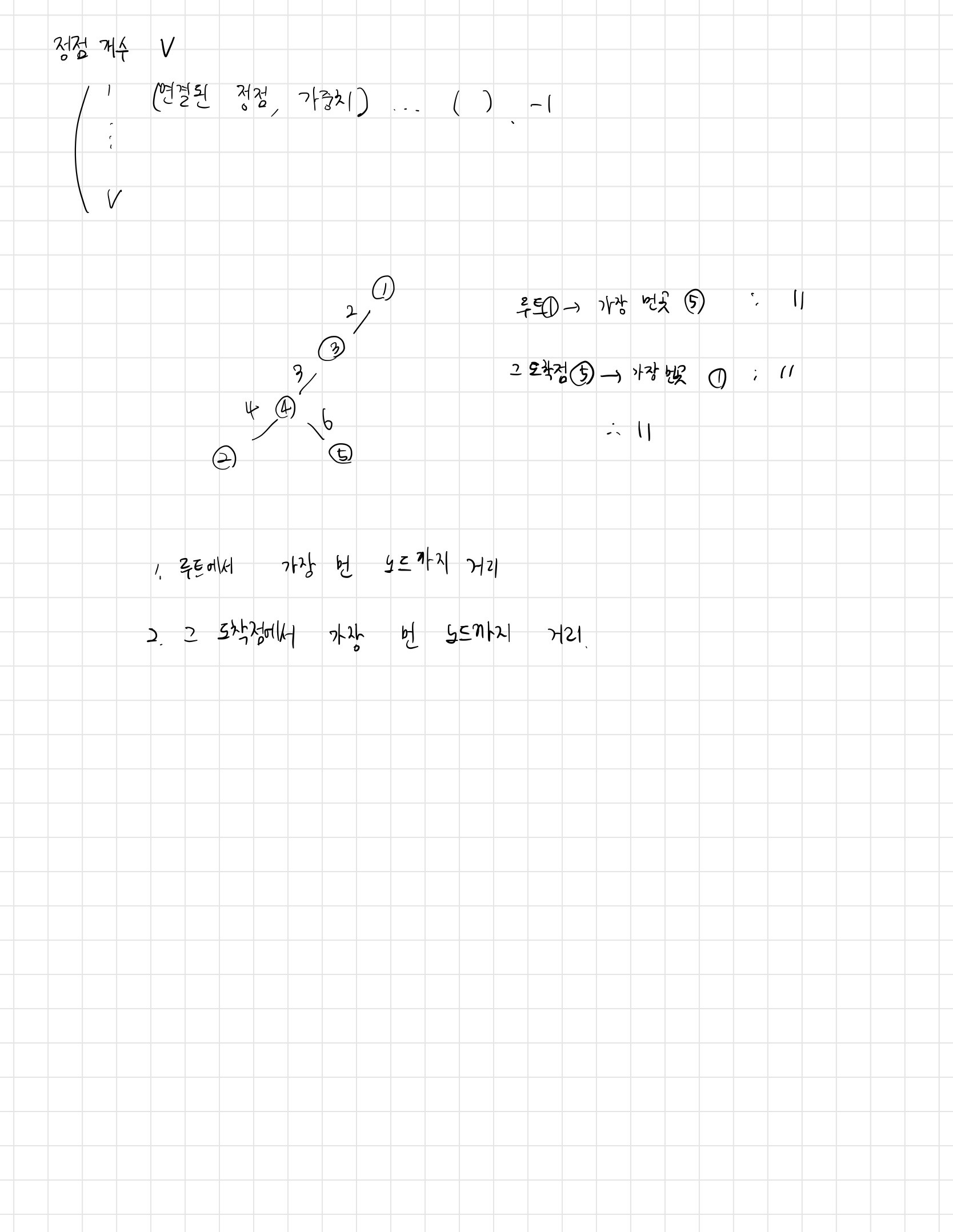
트리가 입력으로 주어진다. 먼저 첫 번째 줄에서는 트리의 정점의 개수 V가 주어지고 (2 ≤ V ≤ 100,000)둘째 줄부터 V개의 줄에 걸쳐 간선의 정보가 다음과 같이 주어진다. 정점 번호는 1부터 V까지 매겨져 있다.

먼저 정점 번호가 주어지고, 이어서 연결된 간선의 정보를 의미하는 정수가 두 개씩 주어지는데, 하나는 정점번호, 다른 하나는 그 정점까지의 거리이다. 예를 들어 네 번째 줄의 경우 정점 3은 정점 1과 거리가 2인 간선으로 연결되어 있고, 정점 4와는 거리가 3인 간선으로 연결되어 있는 것을 보여준다. 각 줄의 마지막에는 -1이 입력으로 주어진다. 주어지는 거리는 모두 10,000 이하의 자연수이다.

출력

첫째 줄에 트리의 지름을 출력한다.

문제 풀이

생각의 전환이 필요했다.

코드

/**
 * Author : nowalex322, Kim HyeonJae
 */
import java.io.*;
import java.util.*;

public class Main {
	static class Node{
		int V;
		int dist;
		public Node(int V, int dist) {
			this.V = V;
			this.dist =  dist;
		}
	}
	
	static BufferedReader br;
	static StringTokenizer st;
	static int N, max, node;
	static ArrayList<Node>[] list;
	static boolean[] visited;
	public static void main(String[] args) throws IOException {
//		br = new BufferedReader(new InputStreamReader(System.in));
		br = new BufferedReader(new InputStreamReader(new FileInputStream("input.txt")));
		
		N = Integer.parseInt(br.readLine());
		list = new ArrayList[N+1];
		for(int i=1; i<=N; i++) {
			list[i] = new ArrayList<Node>();
		}
		for(int i=0; i<N; i++) {
			st = new StringTokenizer(br.readLine());
			int a = Integer.parseInt(st.nextToken());
			while(true) {
				int b = Integer.parseInt(st.nextToken());
				if(b == -1) break;
				int value = Integer.parseInt(st.nextToken());
				list[a].add(new Node(b, value));
			}
		}
		
		visited = new boolean[N + 1];
		dfs(1, 0);
		
		visited = new boolean[N+1];
		dfs(node, 0);
		
		System.out.println(max);
				
		
	}
	private static void dfs(int v, int l) {
		if(l > max) {
			max = l;
			node = v;
		}
		visited[v] = true;
		for(int i=0; i<list[v].size(); i++) {
			Node n = list[v].get(i);
			if(!visited[n.V]) {
				dfs(n.V, n.dist + l);
				visited[n.V] = true;
			}
		}
	}
}