BOJ_17307_색깔 통일하기 (Java)

[Gold II] 색깔 통일하기 - 17307

문제 링크

성능 요약

메모리: 49200 KB, 시간: 432 ms

분류

누적 합

제출 일자

2024년 11월 8일 18:05:43

문제 설명

N개의 버튼이 일렬로 나열되어 있다. 이 버튼들은 바로 양옆에 인접한 버튼끼리 연결되어 있다. 각 버튼은 LED가 내장되어있어 총 C 종류의 색을 띨 수 있다. 그 색깔들을 각각 0번 색깔, 1번 색깔, ..., (C-1)번 색깔이라고 하자.

이때 현재 색깔이 x인 한 버튼을 누르면 누른 버튼과 함께 해당 버튼의 양옆으로 같은 색으로 연속해서 이어진 모든 버튼이 (x+1)%C 번 색깔로 변한다. 우리의 목표는 버튼을 누르는 횟수를 최소화하며 모든 버튼을 같은 색깔로 만드는 것이다.

예를 들어, N=5, C=4일 때 아래와 같은 색의 버튼들이 있다고 하자.

여기서 4번 버튼을 누르면 현재 4번 버튼의 양옆에 같은 색의 버튼이 없으므로 4번 버튼의 색만 0번 색깔로 바뀌게 된다.

그 이후 2번째 버튼을 누르면 2번의 왼쪽으로는 같은 색의 버튼이 없고, 오른쪽으로 연속한 3, 4번 버튼이 2번 버튼의 색과 같으므로 2, 3, 4번 버튼의 색이 1번 색깔로 바뀐다.

그 이후 3번째 버튼을 누르면 1, 2, 3, 4, 5번 버튼의 색이 모두 함께 2번 색깔로 바뀌게 된다.

우리의 목적은 버튼을 누르는 횟수를 최소화 하면서 모든 버튼의 색을 한 색으로 통일시키는 것이다. 위의 방법대로면 4번 버튼을 누른 후 2번 버튼을 누르면서 2회만에 1번 색으로 통일된다.

하지만 지금은 어떤 이유로 오직 하나의 버튼만 누를 수 있기에, 4번 버튼을 누르고 2번 버튼을 누르는 방법은 쓸 수 없게 되었다. 그렇다면 어떤 버튼을 선택해야 해당 버튼을 최소한으로 누르며 모든 버튼의 색을 통일시킬 수 있을까?

입력

첫 번째 줄에 버튼의 수 N(1 ≤ N ≤ 250,000)과 가능한 색의 수 (1 ≤ C ≤ 10⁹)가 공백으로 구분되어 주어진다.

다음 줄에 현재 각 버튼의 색 X_i (0 ≤ X_i < C, 1 ≤ i ≤ N)가 공백으로 구분되어 주어진다.

출력

첫 번째 줄에 몇 번 버튼을 눌러야 하는지 출력한다, 버튼에는 가장 왼쪽에서 시작해 1번부터 N번까지 번호가 차례로 매겨져 있다.

두 번째 줄에 모든 버튼을 같은 색으로 통일시키기 위해 그 버튼을 눌러야 할 횟수를 출력한다. 만약 최소 횟수가 되는 버튼이 여러 개 존재한다면 그중 가장 왼쪽의 버튼을 출력한다.

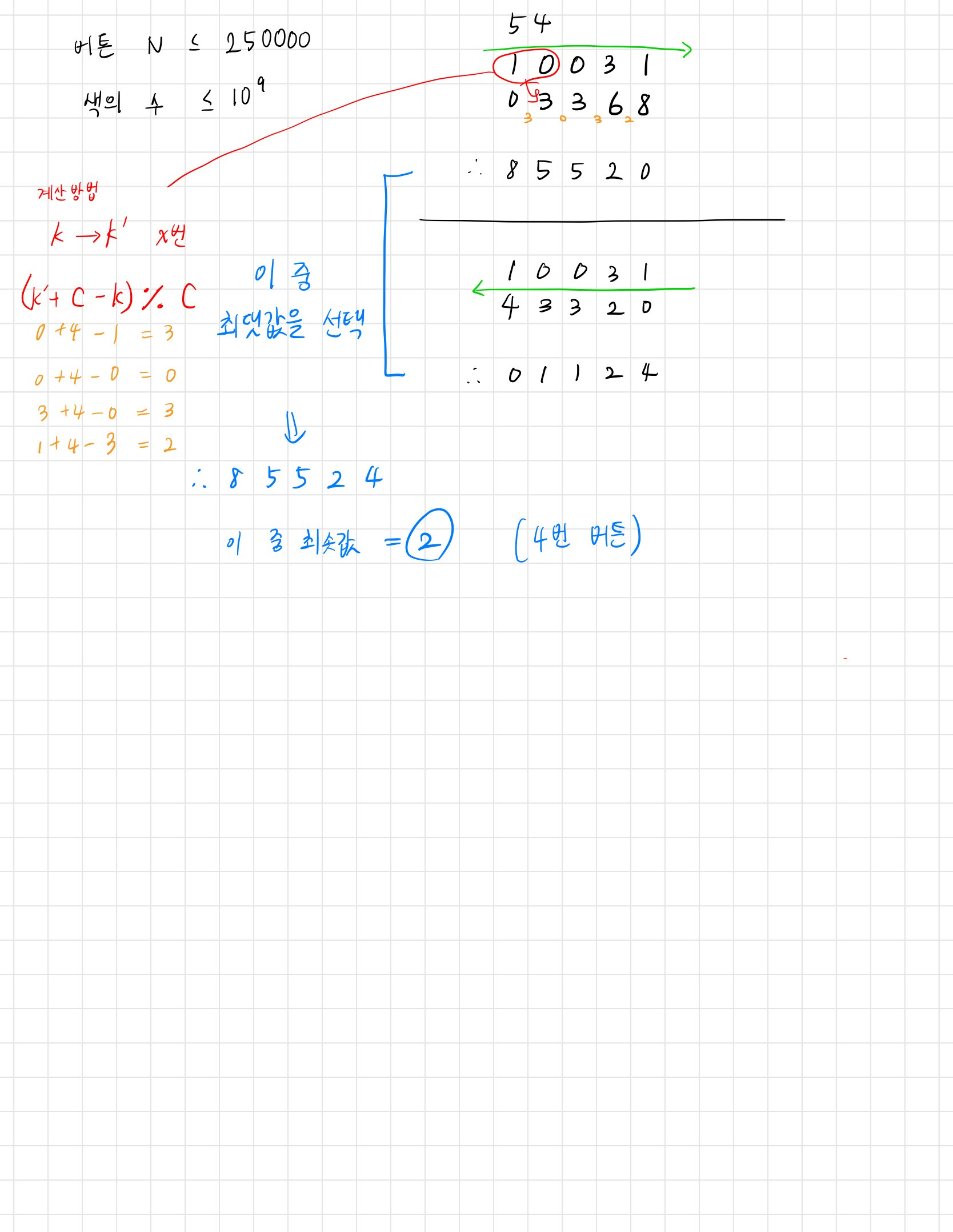
문제 풀이

코드

/**
 * Author: nowalex322, Kim HyeonJae
 */

import java.io.*;
import java.util.*;

public class Main {
	static BufferedReader br;
	static BufferedWriter bw;
	static StringTokenizer st;
	static int N, C, colors[];
	static long rightPrefixSum[], leftPrefixSum[], finalCnt[];
	public static void main(String[] args) throws Exception {
		new Main().solution();
	}

	public void solution() throws Exception {
		br = new BufferedReader(new InputStreamReader(System.in));
//		br = new BufferedReader(new InputStreamReader(new FileInputStream("input.txt")));
		bw = new BufferedWriter(new OutputStreamWriter(System.out));
		st = new StringTokenizer(br.readLine());
		
		N = Integer.parseInt(st.nextToken());
		C = Integer.parseInt(st.nextToken());
		colors = new int[N];
		
		st = new StringTokenizer(br.readLine());
		for(int i=0; i<N; i++) {
			colors[i] = Integer.parseInt(st.nextToken());
		}
		
		rightPrefixSum = new long[N];
		leftPrefixSum = new long[N];
		rightPrefixSum[0] = 0;
		leftPrefixSum[N-1] =0;
		
		for(int i=1; i<N; i++) {
			int y = colors[i];
			int x = colors[i-1];
//			System.out.print(x + " 에서 " + y + " 까지 가는데  ");
			rightPrefixSum[i] = rightPrefixSum[i-1] + calButtonClickCnt(x, y);
//			System.out.println("만큼 걸려");
		}
		
		for(int i=0; i<N; i++) {
			long tmp = rightPrefixSum[i];
			rightPrefixSum[i] = rightPrefixSum[N-1] - tmp;
		}
		
		for(int i=N-2; i>=0; i--) {
			int y = colors[i];
			int x = colors[i+1];
//			System.out.print(x + " 에서 " + y + " 까지 가는데  ");
			leftPrefixSum[i] = leftPrefixSum[i+1] + calButtonClickCnt(x, y);
//			System.out.println(" 만큼 걸려");
		}
		
		for(int i=N-1; i>=0; i--) {
			long tmp = leftPrefixSum[i];
			leftPrefixSum[i] = leftPrefixSum[0] - tmp;
		}
		
		finalCnt = new long[N];
		long res = Long.MAX_VALUE;
		int residx = -1;
		for(int i=0; i<N; i++) {
			finalCnt[i] = Math.max(leftPrefixSum[i], rightPrefixSum[i]);
			if (finalCnt[i] < res) {
	            res = finalCnt[i];
	            residx = i;
	        }
		}
		
//		System.out.println(Arrays.toString(colors));
//		System.out.println(Arrays.toString(rightPrefixSum));
//		System.out.println(Arrays.toString(leftPrefixSum));
//		System.out.println(Arrays.toString(finalCnt));
			
		
		bw.write(String.valueOf(residx+1 + "\n" + res));
		bw.flush();
		bw.close();
		br.close();
	}
	
	private static long calButtonClickCnt(int x, int y) {
//		System.out.print((y+C-x) %C);
		return (y+C-x) %C;
	}
}