BOJ_17387_선분 교차 2 (Java)

[Gold II] 선분 교차 2 - 17387

문제 링크

성능 요약

메모리: 14264 KB, 시간: 100 ms

분류

많은 조건 분기, 기하학, 선분 교차 판정

제출 일자

2024년 10월 14일 04:18:15

문제 설명

2차원 좌표 평면 위의 두 선분 L₁, L₂가 주어졌을 때, 두 선분이 교차하는지 아닌지 구해보자. 한 선분의 끝 점이 다른 선분이나 끝 점 위에 있는 것도 교차하는 것이다.

L₁의 양 끝 점은 (x₁, y₁), (x₂, y₂), L₂의 양 끝 점은 (x₃, y₃), (x₄, y₄)이다.

입력

첫째 줄에 L₁의 양 끝 점 x₁, y₁, x₂, y₂가, 둘째 줄에 L₂의 양 끝 점 x₃, y₃, x₄, y₄가 주어진다.

출력

L₁과 L₂가 교차하면 1, 아니면 0을 출력한다.

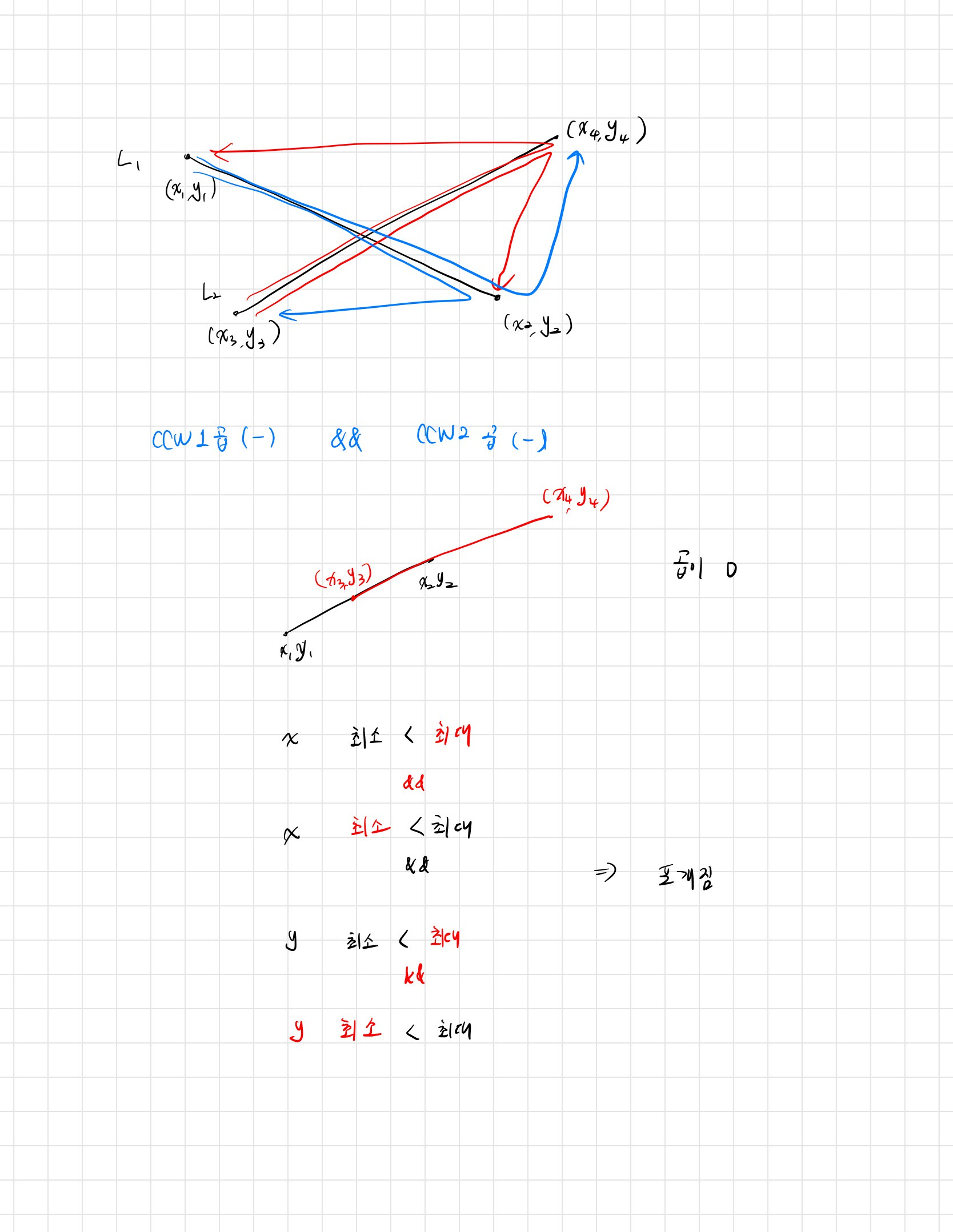
문제 풀이

코드

/**
 * Author: nowalex322, Kim HyeonJae
 */
import java.io.*;
import java.util.*;

public class Main {
	static BufferedReader br;
	static BufferedWriter bw;
	static StringTokenizer st;

	public static void main(String[] args) throws Exception {
		new Main().solution();
	}

	public void solution() throws Exception {
		br = new BufferedReader(new InputStreamReader(System.in));
//		br = new BufferedReader(new InputStreamReader(new FileInputStream("input.txt")));
		bw = new BufferedWriter(new OutputStreamWriter(System.out));
		st = new StringTokenizer(br.readLine());
		long x1 = 0, y1 = 0, x2 = 0, y2 = 0, x3 = 0, y3 = 0, x4 = 0, y4 = 0;
		x1 = Long.parseLong(st.nextToken());
		y1 = Long.parseLong(st.nextToken());
		x2 = Long.parseLong(st.nextToken());
		y2 = Long.parseLong(st.nextToken());

		st = new StringTokenizer(br.readLine());
		x3 = Long.parseLong(st.nextToken());
		y3 = Long.parseLong(st.nextToken());
		x4 = Long.parseLong(st.nextToken());
		y4 = Long.parseLong(st.nextToken());

		int res = isCrossed(x1, y1, x2, y2, x3, y3, x4, y4) ? 1 : 0;
		System.out.println(res);
		bw.flush();
		bw.close();
		br.close();
	}

	private static int ccw(long x1, long y1, long x2, long y2, long x3, long y3) {
		long res = (x1 * y2 + x2 * y3 + x3 * y1) - (x1 * y3 + x2 * y1 + x3 * y2);
		if (res == 0) return 0;
		else if (res > 0) return 1;
		else return -1;
	}

	private static boolean isCrossed(long x1, long y1, long x2, long y2, long x3, long y3, long x4, long y4) {
		int ccw1 = ccw(x1, y1, x2, y2, x3, y3);
		int ccw2 = ccw(x1, y1, x2, y2, x4, y4);
		int ccw3 = ccw(x3, y3, x4, y4, x1, y1);
		int ccw4 = ccw(x3, y3, x4, y4, x2, y2);
		
		if (ccw1 * ccw2 == 0 && ccw3 * ccw4 == 0) {
	        return isOverlap(x1, y1, x2, y2, x3, y3, x4, y4);
	    }

		return (ccw1 * ccw2 <= 0 && ccw3 * ccw4 <= 0);
	}

	private static boolean isOverlap(long x1, long y1, long x2, long y2, long x3, long y3, long x4, long y4) {
		return Math.min(x1, x2) <= Math.max(x3, x4) && Math.min(x3, x4) <= Math.max(x1, x2) &&
		           Math.min(y1, y2) <= Math.max(y3, y4) && Math.min(y3, y4) <= Math.max(y1, y2);
	}
}