BOJ_17510_Bigger Sokoban 40k

[Ruby V] Bigger Sokoban 40k - 17510

문제 링크

성능 요약

메모리: 4528 KB, 시간: 0 ms

분류

해 구성하기

제출 일자

2024년 12월 2일 03:01:22

문제 설명

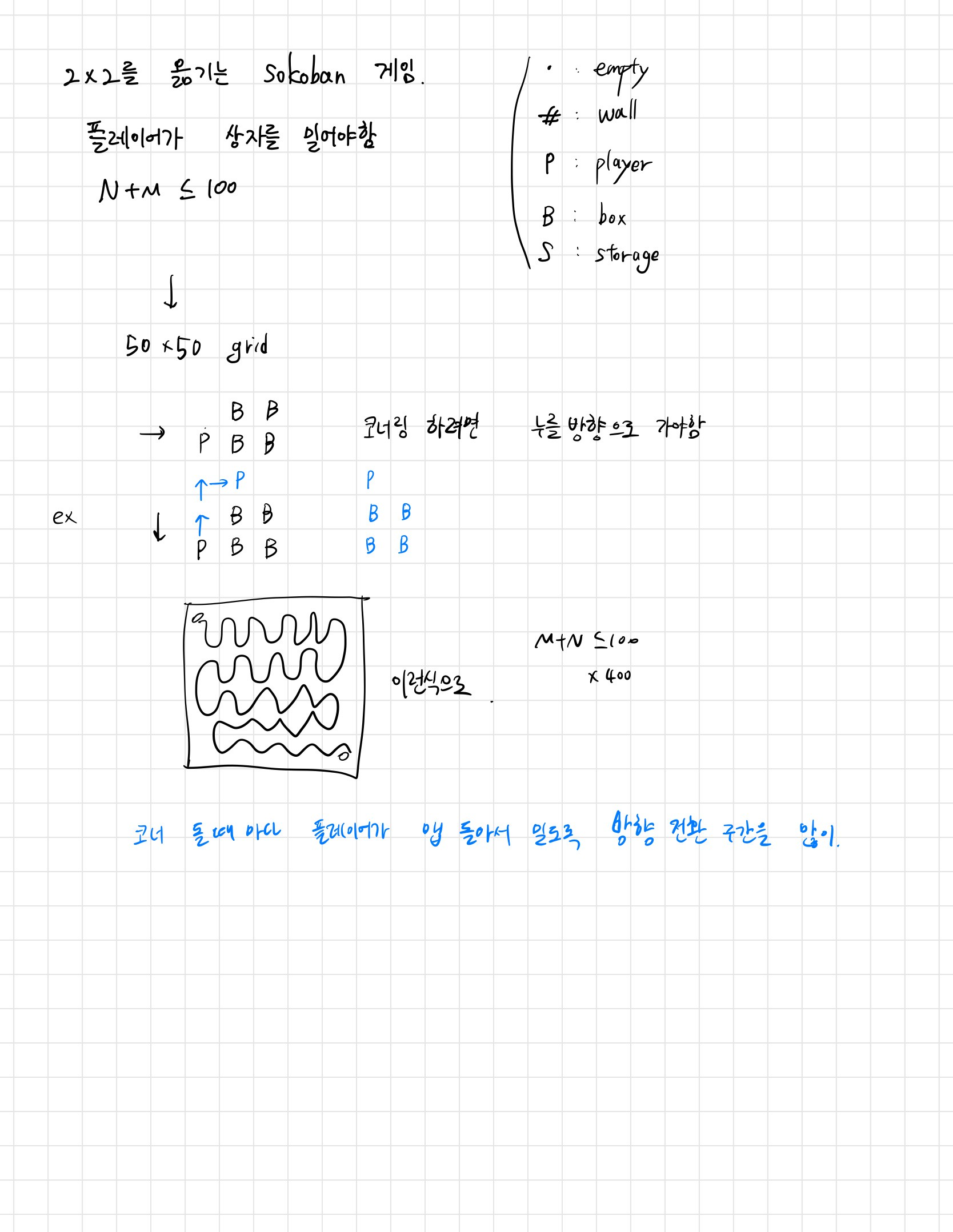
문제 Sokoban is a famous puzzle game, where the player moves around in the $N \times M$-size grid, and pushes $1 \times 1$-size boxes to $1 \times 1$-size storage locations.

Bigger Sokoban is a possible variation of Sokoban, but the size of boxes and storage locations are bigger than $1 \times 1$. This problem especially uses $2 \times 2$ for both.

The rule of Bigger Sokoban is the same as Sokoban. Each square in the grid is an empty square or a wall. Some $2 \times 2$ area of empty squares contain $2 \times 2$-size box each and some $2 \times 2$ area of empty squares are marked as $2 \times 2$-size storage location each.

The player is in the grid and may move up, down, left, right to the adjacent empty squares, but should not go through walls, boxes, or outside of the grid. If the player tries to move into a box, it is pushed to the adjacent squares in that direction. Boxes must not be pushed to other boxes, walls, or outside of the grid, and they cannot be pulled. The number of boxes is equal to the number of storage locations. The puzzle is solved when all boxes are at the storage locations.

Your mission is to make a Bigger Sokoban grid that needs at least 40 000 moves to solve. To make the situation easier, the grid must satisfy the following constraints:

 

• $1 \leq N, \; M, \; N+M \leq 100$.
• The grid contains one box and one storage location.
• The player, the box, and the storage location must not intersect.

입력

There are no inputs for this problem.

출력

In the first line, print two space-separated integers $N,\ M$; they describe the size of the grid.

In each of the following $N$ lines, print a string of length $M$; it describes each row of the grid. Each string must consist of ., #, P, B, S; each character means empty square, wall, player, box, storage location respectively.

The grid must contain exactly one P, exactly four B, and exactly four S. B and S each must form a $2 \times 2$ square. The grid, of course, must be solvable.

Note that the sample output is only to demonstrate a well-formatted output. Since it can be solved in less than 40 000 moves, it is not a correct answer.

문제 풀이

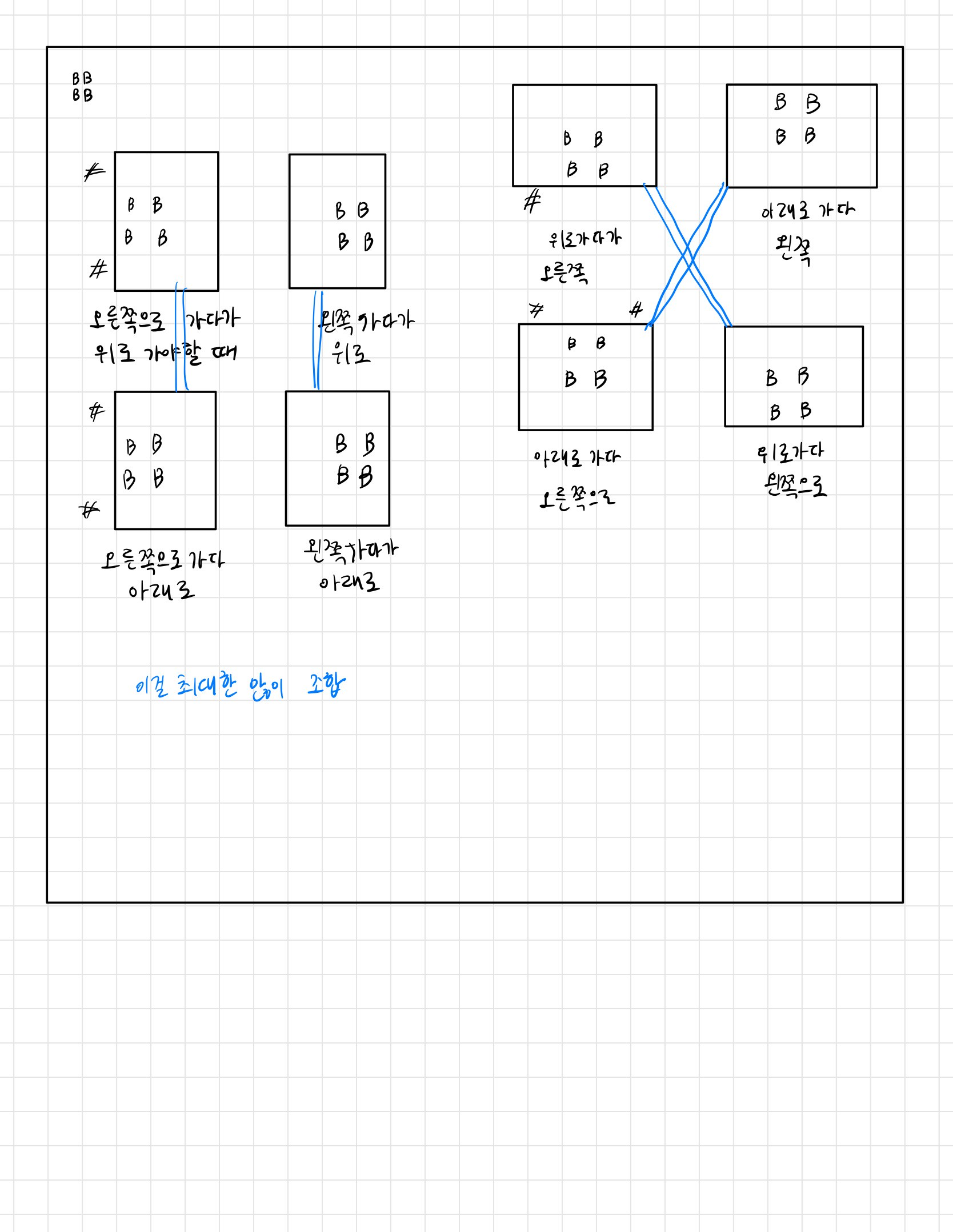
요약그림이다. 일단 N+M이 100이하이므로 50x50그리드를 생각하고 시작했다. 이 안에서 최대한 많은 왕복 (최소 400회)를 해야했는데 그니까 이 그림처럼 꼬불꼬불한 연결되어있는미로를 생각했다. 박스 전후로 이어져있어 박스를 밀려면 다시 돌아가야하는 것이다. 이걸 이용하면 사실 꼬불꼬불한 길을 최대한 꼬불꼬불하게 해서 경로 길이를 늘리고 여러번 왕복시키면 된다. 이때 코너링, 즉 방향을 전환할 때 강제로 경로를 반대로 돌도록 만들었다. 목표는 100개의 코너링을 만드는거였지만 정사각형이 베스트고 이 그리드 크기제한에 의해 90개의 코너링을 만들었다. 그럼 이 경로x90회만큼 이동횟수가 복사가 된다. 이 경로는 길이 약 500정도로 계산하고 만들었는데 나의 목표였던 500x100보다 좀 작은 수준으로 40000을 넘어 성공하도록 만들었다.

코드

#######...#....##...#....##...#....##...#....##...
#BB.......#.........#.........#.........#.........
.BBP......#.........#.........#.........#.........
.######...##..###...##..###...##..###...##..###...
.######..###...##..###...##..###...##..###...##..#
.#####.........#.........#.........#.........##..#
.#####.........#.........#.........#.........##..#
.#####....##...#....##...#....##...#....##...##..#
.##############################################..#
.######...##....#...##....#...##....#...##....#..#
.######.........#.........#.........#.........#..#
.######.........#.........#.........#.........#..#
.######...###..##...###..##...###..##...###..##..#
.#...###..##...###..##...###..##...###..##...##..#
.#.........#.........#.........#.........#.......#
.#.........#.........#.........#.........#........
.#...##....#...##....#...##....#...##....#...#....
.##..#############################################
.##..##...#....##...#....##...#....##...#....##...
.#........#.........#.........#.........#.........
.#........#.........#.........#.........#.........
.#....#...##..###...##..###...##..###...##..###...
.######..###...##..###...##..###...##..###...##..#
.#####.........#.........#.........#.........##..#
.#####.........#.........#.........#.........##..#
.#####....##...#....##...#....##...#....##...##..#
.##############################################..#
.######...##....#...##....#...##....#...##....#..#
.######.........#.........#.........#.........#..#
.######.........#.........#.........#.........#..#
.######...###..##...###..##...###..##...###..##..#
.#...###..##...###..##...###..##...###..##...##..#
.#.........#.........#.........#.........#.......#
.#.........#.........#.........#.........#........
.#...##....#...##....#...##....#...##....#...#....
.##..#############################################
.##..##...#....##...#....##...#....##...#....##...
.#........#.........#.........#.........#.........
.#........#.........#.........#.........#.........
.#....#...##..###...##..###...##..###...##..###...
.######..###...##..###...##..###...##..###...##..#
.#####.........#.........#.........#.........##..#
.#####.........#.........#.........#.........##..#
.#####....##...#....##...#....##...#....##...##..#
.##############################################..#
.#...#...#...#...#...#...#...#...#...#...#...##..#
.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#SS#..#
.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#SS....
.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#......
...#...#...#...#...#...#...#...#...#...#.....#....