BOJ_2162_선분 그룹 (Java)

[Platinum V] 선분 그룹 - 2162

문제 링크

성능 요약

메모리: 19176 KB, 시간: 368 ms

분류

자료 구조, 분리 집합, 기하학, 선분 교차 판정

제출 일자

2024년 9월 22일 14:17:57

문제 설명

N개의 선분들이 2차원 평면상에 주어져 있다. 선분은 양 끝점의 x, y 좌표로 표현이 된다.

두 선분이 서로 만나는 경우에, 두 선분은 같은 그룹에 속한다고 정의하며, 그룹의 크기는 그 그룹에 속한 선분의 개수로 정의한다. 두 선분이 만난다는 것은 선분의 끝점을 스치듯이 만나는 경우도 포함하는 것으로 한다.

N개의 선분들이 주어졌을 때, 이 선분들은 총 몇 개의 그룹으로 되어 있을까? 또, 가장 크기가 큰 그룹에 속한 선분의 개수는 몇 개일까? 이 두 가지를 구하는 프로그램을 작성해 보자.

입력

첫째 줄에 N(1 ≤ N ≤ 3,000)이 주어진다. 둘째 줄부터 N+1번째 줄에는 양 끝점의 좌표가 x1, y1, x2, y2의 순서로 주어진다. 각 좌표의 절댓값은 5,000을 넘지 않으며, 입력되는 좌표 사이에는 빈칸이 하나 있다.

출력

첫째 줄에 그룹의 수를, 둘째 줄에 가장 크기가 큰 그룹에 속한 선분의 개수를 출력한다.

문제 풀이

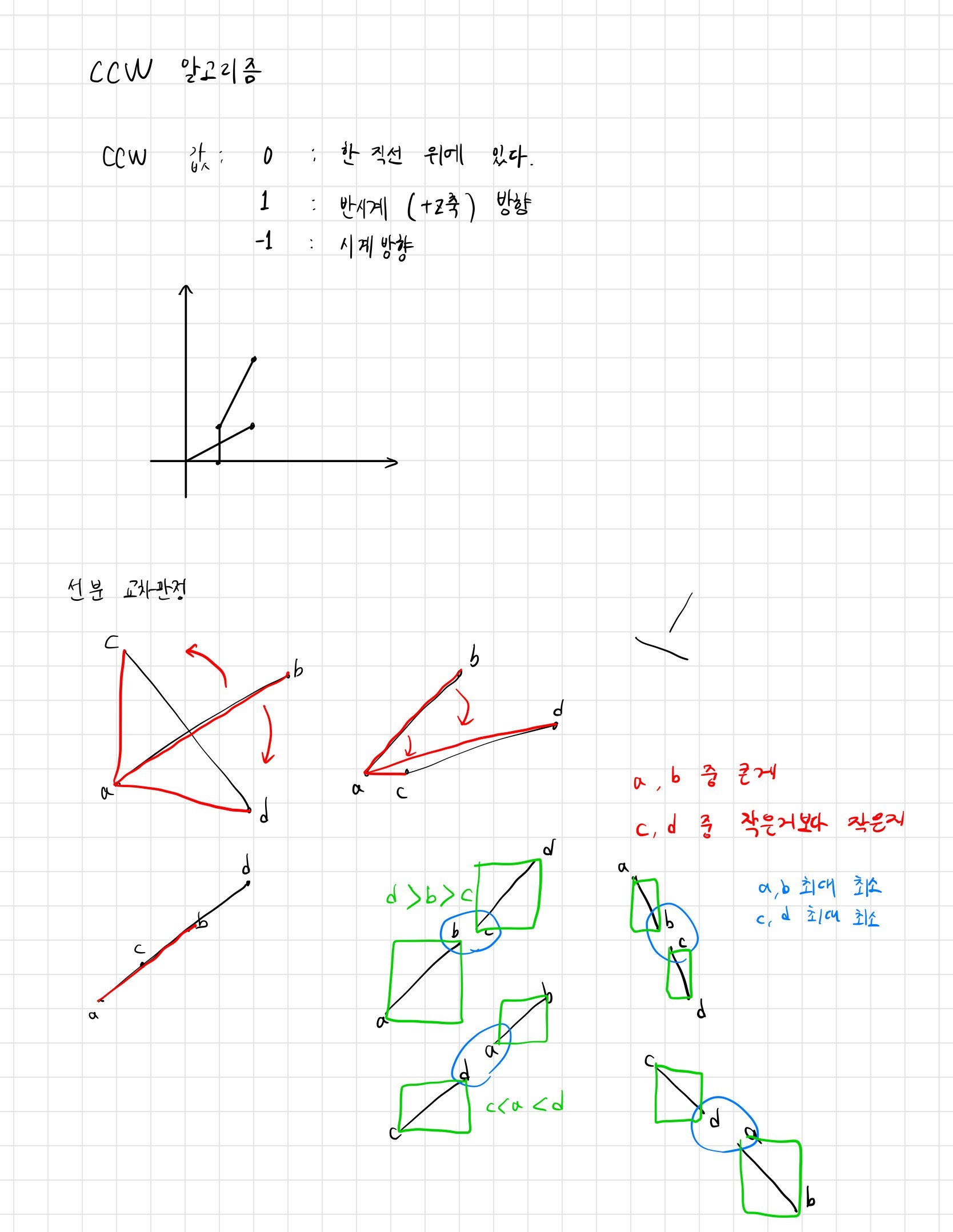
풀이 방법은 쉽게 떠올렸지만 케이스 처리 부분에서 생각을 오래했던 문제. 일자로 두 선분이 나란히 있을때 어떻게 처리해야할 지 , 동 떨어져 있던 두 선분이 새로운 선분에 의해 한 그룹으로 바뀔 때 ( ㅣㅣ 에서 ㅐ 모양 같이 ) 어떻게 처리 할 지 고민을 많이 했다. 경로압축 및 분리집합, 벡터 외적 스칼라곱을 활용해 풀었다.

코드

/**
 * Author: nowalex322, Kim HyeonJae
 */
import java.io.*;
import java.util.*;

public class Main {
	static BufferedReader br;
	static BufferedWriter bw;
	static StringTokenizer st;
	static int N;
	static Line[] lines;
    static Group[] groups;
	public static void main(String[] args) throws Exception {
		new Main().solution();
	}

	public void solution() throws Exception {
		// br = new BufferedReader(new InputStreamReader(System.in));
		br = new BufferedReader(new InputStreamReader(new FileInputStream("input.txt")));
		bw = new BufferedWriter(new OutputStreamWriter(System.out));
		N = Integer.parseInt(br.readLine());

		lines = new Line[N];
        groups = new Group[N];

		for (int i = 0; i < N; i++) {
			st = new StringTokenizer(br.readLine());
			int x1 = Integer.parseInt(st.nextToken());
			int y1 = Integer.parseInt(st.nextToken());
			int x2 = Integer.parseInt(st.nextToken());
			int y2 = Integer.parseInt(st.nextToken());
			lines[i] = new Line(x1, y1, x2, y2);
            groups[i] = new Group(i);
		}
				
		for(int i=0; i<N; i++) {
			for(int j=i+1; j<N; j++) {
				if(isLineCrossed(lines[i], lines[j])) union(i, j);
			}
		}
		
		int groutCnt = 0;
		int maxSize = 0;
		for(int i=0; i<N; i++) {
			if(groups[i].parent == i) {
				groutCnt++;
				maxSize = Math.max(maxSize, groups[i].size);
			}
		}
		
        bw.write(groutCnt + "\n" + maxSize);
		bw.flush();
		bw.close();
		br.close();
	}
	
	private int find(int start) {
		if(groups[start].parent != start) groups[start].parent = find(groups[start].parent);
		return groups[start].parent;
	}
	
	private void union(int start, int end) {
		int root1 = find(start);
		int root2 = find(end);
		
		if(root1 != root2) {
			if (groups[root1].size < groups[root2].size) { // 그룹2에 1을 포함시키기
                groups[root1].parent = root2;
                groups[root2].size += groups[root1].size;
            } else { // 그룹1에 2을 포함시키기
                groups[root2].parent = root1;
                groups[root1].size += groups[root2].size;
            }
		}
	}

	private static int ccw(Point p1, Point p2, Point p3) {
        long res = (p1.x * p2.y + p2.x * p3.y + p3.x * p1.y) - (p1.x * p3.y + p3.x * p2.y + p2.x * p1.y);
		if(res == 0) return 0;
		else if (res > 0) return 1;
		else return -1;
	}
	
	private static boolean isLineCrossed(Line l1, Line l2) {
		Point p1 = l1.p1;
		Point p2 = l1.p2;
		
		Point p3 = l2.p1;
		Point p4 = l2.p2;
		
		int ccw1 = ccw(p1, p2, p3) * ccw(p1, p2, p4);
		int ccw2 = ccw(p3, p4, p1) * ccw(p3, p4, p2);
		
		// 1. 한 줄 일때 
		// 1 3 2 4 처럼 겹칠텐데 1<4 고 2>3 임을 수식으로 작성
		if (ccw1 == 0 && ccw2 == 0) {
            if (Math.min(p1.x, p2.x) <= Math.max(p3.x, p4.x) &&
            	Math.min(p3.x, p4.x) <= Math.max(p1.x, p2.x) && 
            	Math.min(p1.y, p2.y) <= Math.max(p3.y, p4.y) && 
            	Math.min(p3.y, p4.y) <= Math.max(p1.y, p2.y)) {
                return true;
            } 
            else return false;
        } 
		// 2. 크로스가 있을 가능성이 있을 때
		// 2-1. 둘 다 ccw 곱이 음수면 완전 크로스 : true
		else if (ccw1 <= 0 && ccw2 <= 0) return true;
        
		// 그 외는 한쪽 음수 한쪽 양수이므로 ㅡ ㅣ 같은 모양임 : false
		else return false;
        
	}

	class Point implements Comparable<Point>{
		int x, y;

		public Point(int x, int y) {
			this.x = x;
			this.y = y;
		}

		@Override
		public int compareTo(Point o) {
			if(this.x == o.x) return this.y - o.y;
			return this.x - o.x;
		}
	}
	
	class Line{

	    Point p1, p2;

	    public Line(int x1, int y1, int x2, int y2) {
	        Point point1 = new Point(x1, y1);
	        Point point2 = new Point(x2, y2);

	        p1 = point1.compareTo(point2) <= 0 ? point1 : point2;
	        p2 = point1.compareTo(point2) <= 0 ? point2 : point1;
	    }

	}
	
	class Group{
		int parent;
		int size;
		public Group(int parent) {
			this.parent = parent;
			this.size = 1;
		}
	}

}