BOJ_23353_승부 조작 (Java)
[Gold III] 승부 조작 - 23353
성능 요약
메모리: 243664 KB, 시간: 996 ms
분류
다이나믹 프로그래밍
제출 일자
2024년 12월 16일 01:56:03
문제 설명
고양이 랑이와 메리는 오목 게임의 변형인 냥목 게임을 하고 있다. 냥목 게임의 규칙은 복잡하니 점수 계산 방법만 보자.
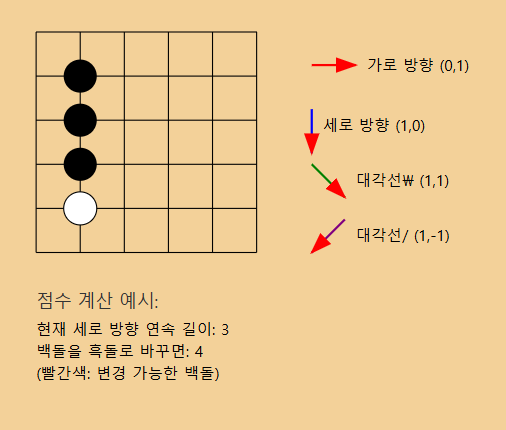
냥목 게임은 위 그림과 같은 $N \times N$ 크기의 바둑판에서 흑돌과 백돌을 이용해 진행된다.
랑이는 흑돌을, 메리는 백돌을 사용한다.
냥목 게임에서 랑이의 점수는 가로, 세로, 대각선 중 하나의 방향으로 연속하여 존재하는 가장 긴 흑돌의 길이가 된다.
잠시 집사가 돌아와서 메리가 반기러 간 사이 랑이는 메리의 돌 하나를 자신의 돌로 바꿔치기 하려고 한다. 즉, 랑이는 백돌 하나를 흑돌로 바꿀 수 있다.
랑이가 백돌 하나를 흑돌로 바꿀 때 얻을 수 있는 최대 점수를 구하는 프로그램을 작성하시오.
랑이는 흑돌을, 메리는 백돌을 사용한다.
냥목 게임에서 랑이의 점수는 가로, 세로, 대각선 중 하나의 방향으로 연속하여 존재하는 가장 긴 흑돌의 길이가 된다.
잠시 집사가 돌아와서 메리가 반기러 간 사이 랑이는 메리의 돌 하나를 자신의 돌로 바꿔치기 하려고 한다. 즉, 랑이는 백돌 하나를 흑돌로 바꿀 수 있다.
랑이가 백돌 하나를 흑돌로 바꿀 때 얻을 수 있는 최대 점수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 자연수 $N$이 주어진다. ($2 \le N \le 1,000$)
둘째 줄부터 $N$개 줄에는 줄마다 $N$개의 숫자가 공백으로 구분되어 주어진다. 이는 랑이가 돌을 바꿔치기하기 전 바둑판의 상태를 나타낸다. 각 수는 0, 1, 2 중 하나로 주어지고, 0은 비어 있는 위치를, 1은 흑돌을, 2는 백돌을 의미한다.
흑돌과 백돌은 각각 하나 이상 존재한다.
출력
랑이가 얻을 수 있는 최대 점수를 출력한다.
문제 풀이
접근 방식
- 4차원 DP 배열 :
r, c: 현재 위치direction: 탐색 방향 (0:가로, 1:세로, 2:대각선, 3:대각선/)changed: 백돌을 바꾼 여부 (0:안바꿈, 1:바꿈)1
static int[][][][] dp; // [r][c][direction][changed]
- 탐색방향배열
1 2
static int[] dr = {0, 1, 1, 1}; // 가로, 세로, 대각선\, 대각선/ static int[] dc = {1, 0, 1, -1};
4가지 방향을 탐색: 가로: (0,1) 세로: (1,0) 대각선: (1,1) 대각선/: (1,-1)
- DP 계산 로직
- 흑돌인 경우: 다음 위치의 DP값에 1을 더합니다 범위를 벗어나면 현재 위치만 계산 (1)
1
2
3
4
5
6
7
8
9
10
11
12
13
if(board[i][j] == 1) { // 흑돌인 경우
for(int k = 0; k < 4; k++) {
int nr = i + dr[k];
int nc = j + dc[k];
if(nr >= 1 && nr <= N && nc >= 1 && nc <= N) {
dp[i][j][k][0] = dp[nr][nc][k][0] + 1;
dp[i][j][k][1] = dp[nr][nc][k][1] + 1;
} else {
dp[i][j][k][0] = 1;
dp[i][j][k][1] = 1;
}
}
}
- 백돌인 경우:
- 한쪽에만 흑돌이 있는 경우: 해당 방향의 연속된 길이 + 1
- 양쪽에 흑돌이 있는 경우: 양쪽 방향의 연속된 길이 합 + 1 (현재 위치)
- 주요 포인트 아래에서 위로(N에서 1로) 탐색하며 DP를 계산! 백돌을 바꾸는 경우, 주변 흑돌과의 연결을 고려해야함. 경계 체크 해야함. 최댓값 갱신.
이 문제의 핵심은 백돌을 바꿨을 때 양쪽의 흑돌 연결을 어떻게 처리하느냐임. 모든 경우(한쪽만 있는 경우, 양쪽 다 있는 경우)를 고려하여 최적의 해를 찾았다.
나중에 다시 풀어보자! 까다로운 dp문제였다
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
else if(board[i][j] == 2) { // 백돌인 경우
for(int k = 0; k < 4; k++) {
int prevR = i - dr[k];
int prevC = j - dc[k];
int nextR = i + dr[k];
int nextC = j + dc[k];
// 이전 방향에 흑돌이 있는 경우
if(prevR >= 1 && prevR <= N && prevC >= 1 && prevC <= N) {
if(board[prevR][prevC] == 1) {
dp[i][j][k][1] = Math.max(dp[i][j][k][1], dp[prevR][prevC][k][0] + 1);
}
}
// 다음 방향에 흑돌이 있는 경우도 동일하게 처리
// 양쪽 모두 흑돌이 있는 경우
if(prevR >= 1 && ... && board[prevR][prevC] == 1 && board[nextR][nextC] == 1) {
dp[i][j][k][1] = dp[prevR][prevC][k][0] + dp[nextR][nextC][k][0] + 1;
}
}
}
코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
/**
* Author: nowalex322, Kim HyeonJae
*/
import java.io.*;
import java.util.*;
public class Main {
static BufferedReader br;
static BufferedWriter bw;
static StringTokenizer st;
static int N, res=0;
static int[] dr = {0, 1, 1, 1}; // 가로, 세로, 대각선\, 대각선/
static int[] dc = {1, 0, 1, -1};
static int[][] board;
static int[][][][] dp; // [r][c][direction][changed]
public static void main(String[] args) throws Exception {
new Main().solution();
}
public void solution() throws Exception {
br = new BufferedReader(new InputStreamReader(System.in));
// br = new BufferedReader(new InputStreamReader(new FileInputStream("input.txt")));
bw = new BufferedWriter(new OutputStreamWriter(System.out));
N = Integer.parseInt(br.readLine());
board = new int[N+2][N+2];
// (r, c) 위치에서 k방향으로 연속된 흑돌의 최대 길이
dp = new int[N+2][N+2][4][2]; // direction: 0-가로, 1-세로, 2-대각선\, 3-대각선/, changed: 0-안바꿈, 1-바꿈
List<int[]> whiteList = new ArrayList<>();
for(int i = 1; i <= N; i++) {
st = new StringTokenizer(br.readLine());
for(int j = 1; j <= N; j++) {
board[i][j] = Integer.parseInt(st.nextToken());
if(board[i][j] == 2) whiteList.add(new int[] {i, j});
}
}
// dp 계산
for(int i = N; i >= 1; i--) {
for(int j = N; j >= 1; j--) {
if(board[i][j] == 1) {
for(int k = 0; k < 4; k++) {
int nr = i + dr[k];
int nc = j + dc[k];
if(nr >= 1 && nr <= N && nc >= 1 && nc <= N) {
dp[i][j][k][0] = dp[nr][nc][k][0] + 1;
dp[i][j][k][1] = dp[nr][nc][k][1] + 1;
} else {
dp[i][j][k][0] = 1;
dp[i][j][k][1] = 1;
}
}
}
else if(board[i][j] == 2) {
for(int k = 0; k < 4; k++) {
int prevR = i - dr[k];
int prevC = j - dc[k];
int nextR = i + dr[k];
int nextC = j + dc[k];
if(prevR >= 1 && prevR <= N && prevC >= 1 && prevC <= N) {
if(board[prevR][prevC] == 1) {
// 이전 방향에 흑돌이 있는 경우
dp[i][j][k][1] = Math.max(dp[i][j][k][1], dp[prevR][prevC][k][0] + 1);
}
}
if(nextR >= 1 && nextR <= N && nextC >= 1 && nextC <= N) {
if(board[nextR][nextC] == 1) {
// 다음 방향에 흑돌이 있는 경우
dp[i][j][k][1] = Math.max(dp[i][j][k][1], dp[nextR][nextC][k][0] + 1);
}
}
// 양쪽 모두 흑돌이 있는 경우
if(prevR >= 1 && prevR <= N && prevC >= 1 && prevC <= N &&
nextR >= 1 && nextR <= N && nextC >= 1 && nextC <= N &&
board[prevR][prevC] == 1 && board[nextR][nextC] == 1) {
dp[i][j][k][1] = dp[prevR][prevC][k][0] + dp[nextR][nextC][k][0] + 1;
}
}
}
}
}
// 최대값 찾기
int res = 0;
for(int i = 1; i <= N; i++) {
for(int j = 1; j <= N; j++) {
for(int k = 0; k < 4; k++) {
res = Math.max(res, Math.max(dp[i][j][k][0], dp[i][j][k][1]));
}
}
}
System.out.println(res);
bw.flush();
bw.close();
br.close();
}
}