BOJ_24230_트리 색칠하기 (Java)

[Gold V] 트리 색칠하기 - 24230

문제 링크

성능 요약

메모리: 105944 KB, 시간: 1624 ms

분류

깊이 우선 탐색, 그래프 이론, 그래프 탐색, 트리

제출 일자

2025년 2월 16일 20:52:11

문제 설명

정점이 $N$개인 트리가 있다. 정점에는 1부터 $N$까지 번호가 붙어있다. 트리의 루트는 항상 1번 정점이며 맨 처음에는 모든 정점이 하얀색으로 칠해져 있는 상태이다.</p>

하나의 정점에 색칠하면 해당 정점 아래 있는 모든 정점이 같은 색으로 칠해진다. 색은 섞이지 않고 색칠할 때마다 그 색으로 덮어진다. 단, 하얀색으로 색칠할 수는 없다.

아래 그림처럼 정점 10개로 구성된 트리가 있다고 가정을 해보자.

[그림 1] 하얀색으로 칠해져 있는 트리

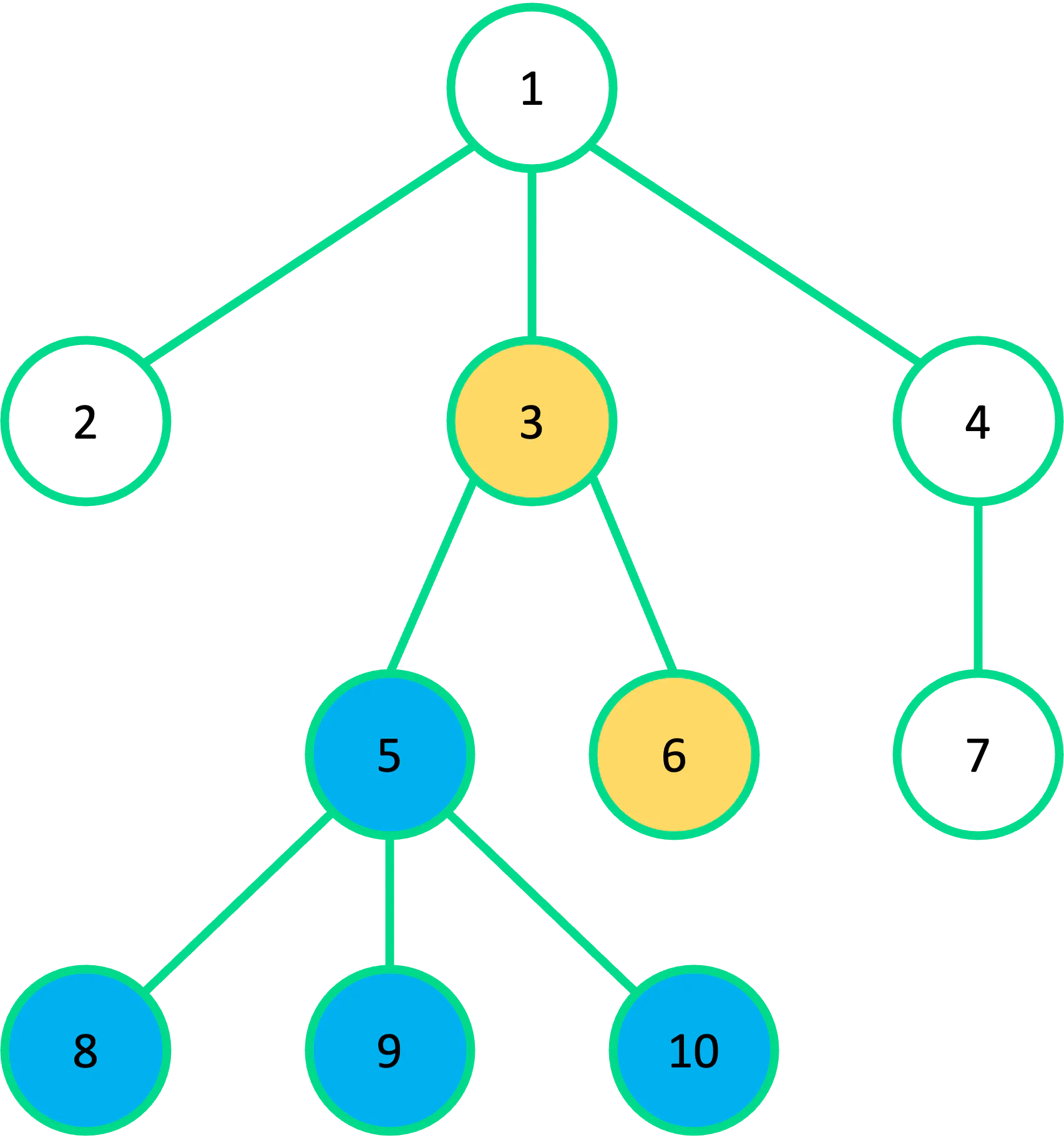
3번 정점을 노란색으로 칠하면 그 아래 있는 정점 5, 6, 8, 9, 10 모두 노란색으로 칠해진다.

[그림 2] 정점 3에 노란색을 칠한 후 트리의 상태

그리고 정점 5에 파란색을 칠한다면 그 아래 있는 정점 8, 9, 10 모두 파란색으로 칠해진다.

[그림 3] 정점 5에 파란색을 칠한 후 트리의 상태

입력으로 트리의 정보와 정점의 색 정보가 주어진다. 색 정보는 음이 아닌 정수로 주어지며 값이 0인 경우는 항상 하얀색을 의미한다.

하얀색을 제외한 색만 사용해서 모든 정점을 주어진 색으로 칠하고 싶을 때 최소 몇 번 색을 칠해야 모든 정점을 원하는 색으로 칠할 수 있는지 구해보자.

입력

첫째 줄에 트리를 구성하는 정점의 개수 $N(1 ≤ N ≤ 200,000)$이 주어진다.

둘째 줄에 1번 정점부터 $N$번 정점까지 각 색 정보 $C_i (0 ≤ C_i ≤ N)$가 공백으로 구분되어 주어진다.

셋째 줄부터 $N - 1$개의 줄에 걸쳐 연결된 두 정점 $a, b(1 ≤ a, b ≤ N$, $a ≠ b)$가 공백으로 구분되어 주어진다.

모든 정점을 칠할 수 있는 입력만 주어진다.

출력

하얀색을 제외한 색만 사용해서 모든 정점을 원하는 색으로 칠하기 위해 최소 몇 번 칠하면 되는지 출력한다.

문제풀이

위에서부터 dfs로 색칠하면된다.

코드

/**
 * Author: nowalex322, Kim HyeonJae
 */

import java.io.*;
import java.util.*;

public class Main {
    static BufferedReader br;
    static BufferedWriter bw;
    static StringTokenizer st;
    static int N, node, a, b, res;
    static int[] colors;
    static List<Integer>[] tree;
    public static void main(String[] args) throws Exception {
        new Main().solution();
    }

    public void solution() throws Exception {
        br = new BufferedReader(new InputStreamReader(System.in));
//        br = new BufferedReader(new InputStreamReader(new FileInputStream("src/main/java/BOJ_24230_트리색칠하기/input.txt")));
        bw = new BufferedWriter(new OutputStreamWriter(System.out));

        N = Integer.parseInt(br.readLine());
        colors = new int[N+1];
        st = new StringTokenizer(br.readLine());
        for(int i=1; i<=N; i++) {
            colors[i] = Integer.parseInt(st.nextToken());
        }

        tree = new ArrayList[N+1];
        for(int i=1; i<=N; i++) {
            tree[i] = new ArrayList<>();
        }

        for(int i=0; i<N-1; i++) {
            st = new StringTokenizer(br.readLine());
            a = Integer.parseInt(st.nextToken());
            b = Integer.parseInt(st.nextToken());
            tree[a].add(b);
            tree[b].add(a);
        }

        dfs(1, 0, 0);

        System.out.println(res);
        bw.flush();
        bw.close();
        br.close();
    }

    private void dfs(int curr, int parent, int color) {
        if(colors[curr] != colors[parent]) res++;

        for(int node : tree[curr]) {
            if(node != parent) dfs(node, curr, colors[curr]);
        }
    }
}