BOJ_2549_루빅의 사각형 (Java)

Posted Feb 9, 2025

By Hyeon Jae Kim

18 min read

[Platinum II] 루빅의 사각형 - 2549

문제 링크

성능 요약

메모리: 86480 KB, 시간: 424 ms

분류

백트래킹, 양방향 탐색, 그래프 이론, 중간에서 만나기

제출 일자

2025년 2월 9일 02:42:05

문제 설명

4×4 격자판에 1에서 16까지 정수 번호가 매겨진 16개 타일이 임의로 놓여져 있다. 타일을 움직여 그림 1과 같이 타일을 놓이게 하려고 한다.

1	2	3	4
5	6	7	8
9	10	11	12
13	14	15	16

그림 1

타일을 움직이는 방법은 하나의 행(가로줄)을 오른쪽으로 원하는 칸 수만큼 순환적으로 움직이거나, 하나의 열(세로줄)을 원하는 칸 수만큼 아래쪽으로 순환적으로 움직이는 것이다. 그림 2는 그림 1의 2번째 행을 오른쪽으로 2칸 움직인 것이다. 그림 1의 2번째 행의 오른쪽 끝에 있는 7번 타일과 8번 타일이 오른쪽 경계를 넘어가서 왼쪽 끝으로 옮겨갔다.

1	2	3	4
7	8	5	6
9	10	11	12
13	14	15	16

그림 2

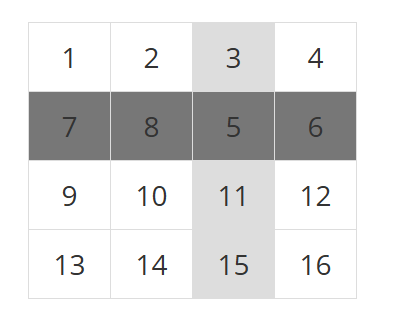
그림 3은 그림 2의 3번째 열을 아래쪽으로 1칸 움직인 것이다. 그림 2의 3번째 열의 가장 아래에 있는 15번 타일이 가장 위쪽으로 옮겨갔다.

1	2	15	4
7	8	3	6
9	10	5	12
13	14	11	16

그림 3

그림 3과 같이 타일이 놓여진 격자판이 주어졌다면 3번째 열을 3칸 움직인 다음, 2번째 행을 2칸 움직이면 그림 1과 같이 타일이 놓이게 된다. 따라서 2번 움직이면 된다.

1에서 16까지 번호가 매겨진 타일이 임의로 놓여져 있을 때 그림 1과 같이 타일이 놓일 수 있도록 타일을 움직이는 순서를 출력하는 프로그램을 작성하시오. 여기서 움직이는 횟수는 최소로 하여야 한다.

입력

4×4 격자판에 놓여진 타일 번호가 행단 위로 4개 줄에 주어진다. 타일 번호는 1부터 16까지의 정수이다.

각 줄에는 해당하는 행에 놓여지는 4개 타일의 번호가 빈칸을 사이에 두고 순서대로 주어진다.

출력

첫 번째 줄에는 움직이는 횟수를, 두 번째 줄부터는 한 줄에 하나씩 타일을 움직이는 방법을 순서대로 출력한다.

이때, 격자판의 i번째 행을 k칸 움직였다면 정수 1과 i와 k를 빈칸을 사이에 두고 한 줄에 출력한다. 그리고 격자판의 i번째 열을 k칸 움직였다면 정수 2와 i와 k를 빈칸을 사이에 두고 한 줄에 출력한다. 여기서 i는 1 이상 4 이하, k는 1 이상 3 이하의 정수이다.

문제 풀이

한 줄 이동에 3가지 방법이 있다. 그러므로 8개의 선이 있으므로 24개의 방법이라고 할 수 있다. 완전탐색이면 최대 7번이라고 할 때 24^7 가지의 상태가 발생할 수 있고 약 40억개이므로 시간초과가 발생한다.

이에 2가지 방법이 정해라고 생각된다.

양방향 탐색 : O(24^3.5)

각 방향에서 24^3.5 번 탐색하므로 약 100만번의 연산이므로 가능하다.

휴리스틱을 이용한 가지치기 : 최악 O(24^7) 틀린 개수를 기반으로 가지치기 하기 때문에 실제 탐색에서 많이 감소된다. 예를들어 틀린 개수가 4개라고 해서 반드시 1번의 이동으로 해결되는 것은 아니지만 꽤나 많은 경우 1번으로 해결되고, 틀린갯수고 7개라고 해서 반드시 2번의 이동으로 해결되지는 않지만 꽤나 추정이 정확하다는 점에서, 이를 가지치기로 사용한다. 현재까지 이동횟수 + 예상필요이동횟수의 합이 지금까지의 최적해보다 크거나 같아지면 백트래킹을 하는 방식으로 말이다. 이렇게 실제로 정확하지는 않지만 가지치기를 많이 할 수 있기 때문에 휴리스틱도 가능하다.

1번 방법으로 생각해보자. 먼저 보드의 상태와 그 상태를 만들기위한 이동 경로를 저장해야하고 다른 클래스로 각 이동을 표현해야한다. 양방향 탐색은 시작 상태에서 정방향으로 bfs, 목표상태에서 역방향으로 bfs를 하여 중간에 두 탐색이 만나는 지점이 생기면 경로를 구성할 수 있다.

이 두 경로를 합치면서 역방향 이동은 반대방향으로 바꾸면 완전한 경로가 나온다.

구현 설명

1. 상태 클래스 (State)

각 보드의 상태와 그 상태에 도달하기까지의 이동경로를 저장하는 클래스

        
      
class State {
    int[][] board;  // 4x4 보드 상태
    List<Move> moves;  // 이동 경로

    // 깊은 복사를 위한 생성자
    public State(int[][] board, List<Move> moves) {
        this.board = new int[4][4];
        for(int i = 0; i < 4; ++i) {
            this.board[i] = Arrays.copyOf(board[i], 4);
        }
        this.moves = new ArrayList<>(moves);
    }
}

방문 체크를 위해 equals와 hashCode를 오버라이드했다. 보드의 상태만을 비교하며 이동경로는 비교하지 않는다.

2. 이동 클래스 (Move)

각각의 이동을 표현하는 클래스이다.

        
      
class Move {
    int type;  // 1: 가로줄 오른쪽, 2: 세로줄 아래쪽
    int idx;   // 0-based로 몇 번째 줄인지
    int cnt;   // 몇 칸 이동하는지
}

3. 양방향 BFS 구현

양방향 BFS :

시작점에서 출발하는 정방향 큐와 목표점에서 출발하는 역방향 큐를 운영
각 방향별로 방문 체크를 위한 맵을 따로 관리
각 단계마다 양쪽에서 한 번씩 탐색을 진행
두 탐색이 만나는 지점이 발견되면 경로를 구성

3-1. search 메서드

BFS의 메인 로직을 담당하는 메서드로 다음과 같이 동작 :

양방향 탐색을 위한 자료구조 초기화
- 정방향 큐(forwardQueue)와 역방향 큐(backwardQueue)
- 정방향 방문맵(forwardVisited)와 역방향 방문맵(backwardVisited)

초기 상태 설정

        
State initialState = new State(initialBoard, new ArrayList<>());
State targetState = new State(targetBoard, new ArrayList<>());

양방향 탐색 수행
- 정방향 탐색 수행 → expandSearch(forwardQueue, …)
- 역방향 탐색 수행 → expandSearch(backwardQueue, …)
- 두 탐색이 만나는 지점을 발견하면 경로 재구성

3-2. expandSearch 메서드

search 메서드에서 호출되는 실제 탐색을 수행하는 메서드 :

큐에서 현재 상태를 꺼낸다
가능한 모든 이동(24가지)을 시도한다
- 2가지 타입 (가로/세로)
- 4개의 줄
- 3가지 이동 칸수
각 이동에 대해:
- 새로운 보드 상태 생성
- 방문하지 않은 상태면 큐에 추가
- 다른 방향 탐색과 만나는지 체크

만나는 지점 발견시 해당 상태 반환, 없으면 null 반환

4. 이동 처리 (moveBoard)

보드의 이동은 다음과 같이 처리한다:

가로 이동의 경우 해당 행을 순환적으로 이동
세로 이동의 경우 해당 열을 순환적으로 이동

나머지 위치는 그대로 유지

        
      
private int[][] moveBoard(int[][] board, int type, int idx, int cnt) {
  // 깊은 복사
  int[][] newBoard = new int[N][N];
  for(int i=0; i<N; ++i) {
      newBoard[i] = Arrays.copyOf(board[i], N);
  }

  if(type == 1) {  // 가로 이동
      int[] tmp = new int[N];
      for(int c=0; c<N; c++) {
          tmp[(c+cnt) % 4] = board[idx][c];
      }
      newBoard[idx] = tmp;
  } else {  // 세로 이동
      int[] tmp = new int[N];
      for(int r=0; r<N; r++) {
          tmp[(r+cnt) % 4] = board[r][idx];
      }
      for(int r=0; r<N; r++) {
          newBoard[r][idx] = tmp[r];
      }
  }
  return newBoard;
}

5. 경로 재구성 (remakePath)

두 방향의 탐색이 만나면 경로를 다음과 같이 재구성 :

정방향 경로는 그대로 사용
역방향 경로는 반대로 뒤집어서 붙임
역방향 이동은 반대 방향으로 변환 (4-cnt 칸 이동)

        
      
List<Move> remakePath(State meetingState, Map<String, State> forwardVisited, Map<String, State> backwardVisited) {
    String boardString = boardToString(meetingState.board);
    List<Move> forwardMoves = forwardVisited.get(boardString).moves;
    List<Move> backwardMoves = backwardVisited.get(boardString).moves;

    List<Move> totalPath = new ArrayList<>(forwardMoves);
    for(int i=backwardMoves.size()-1; i>=0; i--) {
        Move move = backwardMoves.get(i);
        totalPath.add(new Move(move.type, move.idx, 4 - move.cnt));
    }
    return totalPath;
}

시간복잡도

각 상태에서 24가지의 이동이 가능하다. 양방향 BFS를 사용하므로 24^(d/2)개의 상태만 탐색한다. (d는 최단거리) 따라서 시간복잡도는 O(24^3.5)이다.

공간복잡도

각 상태는 16개의 정수와 이동경로를 저장한다. 최대 24^3.5개의 상태를 저장한다. 따라서 공간복잡도는 O(24^3.5)이다.

코드

        
      
package BOJ_2549_루빅의사각형;
        
/**
 * Author: nowalex322, Kim HyeonJae
 */

import java.io.*;
import java.util.*;

public class Main {
    class State{
        int[][] board;
        List<Move> moves;

        public State(int[][] board, List<Move> moves){
            this.board = new int[4][4];
            for(int i = 0; i < 4; ++i){
                this.board[i] = Arrays.copyOf(board[i], 4);
            }
            this.moves = new ArrayList<>(moves);
        }

        @Override
        public boolean equals(Object o){
            if(this == o) return true;
            if(!(o instanceof State)) return false;
            State other = (State)o;
            for(int i = 0; i < 4; ++i){
                if(!Arrays.equals(this.board[i], other.board[i])) return false;
            }
            return true;
        }

        @Override
        public int hashCode(){
            return Arrays.deepHashCode(board);
        }
    }

    class Move{
        int type; // 1 : 오른쪽으로밀기, 2 : 아래로밀기
        int idx; // 0-based
        int cnt; // 이동한 칸 수
        public Move(int type, int idx, int cnt){
            this.type = type;
            this.idx = idx;
            this.cnt = cnt;
        }
    }

    static BufferedReader br;
    static BufferedWriter bw;
    static StringTokenizer st;
    static final int N = 4;
    static int[][] initialBoard, targetBoard;
    public static void main(String[] args) throws Exception {
        new Main().solution();
    }

    public void solution() throws Exception {
//        br = new BufferedReader(new InputStreamReader(System.in));
        br = new BufferedReader(new InputStreamReader(new FileInputStream("src/main/java/BOJ_2549_루빅의사각형/input.txt")));
        bw = new BufferedWriter(new OutputStreamWriter(System.out));

        // 시작보드
        initialBoard = new int[N][N];
        for(int i = 0; i < N; ++i){
            st = new StringTokenizer(br.readLine());
            for(int j = 0; j < N; ++j){
                initialBoard[i][j] = Integer.parseInt(st.nextToken());
            }
        }

        // 완성할 보드
        targetBoard = new int[N][N];
        int num = 1;
        for(int i = 0; i < N; ++i){
            for(int j = 0; j < N; ++j){
                targetBoard[i][j] = num++;
            }
        }

        // 양방향탐색
        List<Move> sol = search(initialBoard);

        System.out.println(sol.size());
        for(Move m : sol){
            System.out.println(m.type + " " + (1+m.idx) + " " + m.cnt);
        }
        bw.flush();
        bw.close();
        br.close();
    }

    private List<Move> search(int[][] initialBoard){
        Queue<State> forwardQueue = new LinkedList<>();
        Queue<State> backwardQueue = new LinkedList<>();
        Map<String, State> forwardVisited = new HashMap<>();
        Map<String, State> backwardVisited = new HashMap<>();

        State initialState = new State(initialBoard, new ArrayList<>());
        State targetState = new State(targetBoard, new ArrayList<>());

        forwardQueue.offer(initialState);
        backwardQueue.offer(targetState);
        forwardVisited.put(boardToString(initialBoard), initialState);
        backwardVisited.put(boardToString(targetBoard), targetState);

        while(!forwardQueue.isEmpty() && !backwardQueue.isEmpty()){
            // 정방향
            State meetingState = expandSearch(forwardQueue, forwardVisited, backwardVisited, true);

            if(meetingState != null) return remakePath(meetingState, forwardVisited, backwardVisited);

            // 역방향
            meetingState = expandSearch(backwardQueue, backwardVisited, forwardVisited, false);

            if(meetingState != null) return remakePath(meetingState, forwardVisited, backwardVisited);

        }
        return new ArrayList<>(); // 못 찾았을때
    }

    private State expandSearch(Queue<State> queue, Map<String, State> visited, Map<String, State> otherVisited, boolean ifForward){
        State curr = queue.poll();

        //모든방법 시도
        for(int type=1; type<=2; type++){
            for(int idx=0; idx<4; idx++){
                for(int cnt=1; cnt<=3; cnt++){
                    int[][] newBoard = moveBoard(curr.board, type, idx, cnt);
                    List<Move> newMoves = new ArrayList<>(curr.moves);
                    newMoves.add(new Move(type, idx, cnt));

                    State newState = new State(newBoard, newMoves);
                    String boardString = boardToString(newBoard);

                    if(!visited.containsKey(boardString)){
                        visited.put(boardString, newState);
                        queue.offer(newState);

                        // 다른방향 탐색이랑 만나는지 체크
                        if(otherVisited.containsKey(boardString)){
                            return newState;
                        }
                    }
                }
            }
        }
        return null;
    }

    private int[][] moveBoard(int[][] board, int type, int idx, int cnt){
        int[][] newBoard = new int[N][N];
        for(int i=0; i<N; ++i){
            newBoard[i] = Arrays.copyOf(board[i], N);
        }

        // 가로오른쪽으로
        if(type == 1){
            int[] tmp = new int[N];
            for(int c=0; c<N; c++){
                tmp[(c+cnt) % 4] = board[idx][c];
            }
            newBoard[idx] = tmp;
        }
        // 세로아래로
        else{
            int[] tmp = new int[N];
            for(int r=0; r<N; r++){
                tmp[(r+cnt) % 4] = board[r][idx];
            }
            for(int r=0; r<N; r++){
                newBoard[r][idx] = tmp[r];
            }
        }
        return newBoard;
    }

    String boardToString(int[][] board){
        StringBuilder sb = new StringBuilder();
        for(int i=0; i<N; ++i){
            for(int j=0; j<N; ++j){
                sb.append(board[i][j]).append(" ");
            }
        }
        return sb.toString();
    }

    List<Move> remakePath(State meetingState, Map<String, State> forwardVisited, Map<String, State> backwardVisited){
        String boardString = boardToString(meetingState.board);
        List<Move> forwardMoves = forwardVisited.get(boardString).moves;
        List<Move> backwardMoves = backwardVisited.get(boardString).moves;

        List<Move> totalPath = new ArrayList<>(forwardMoves);
        // 역방향을 반대로 붙이기
        for(int i=backwardMoves.size()-1; i>=0; i--){
            Move move = backwardMoves.get(i);
            // 반대방향 이동은 4-cnt칸 이동임
            totalPath.add(new Move(move.type, move.idx, 4 - move.cnt));
        }
        return totalPath;
    }
}

알고리즘

Java 백준 알고리즘

This post is licensed under CC BY 4.0 by the author.