BOJ_32031_석고모형만들기 (Java)

[Gold II] 석고 모형 만들기 - 32031

문제 링크

성능 요약

메모리: 24888 KB, 시간: 212 ms

분류

너비 우선 탐색, 자료 구조, 분리 집합, 플러드 필, 기하학, 3차원 기하학, 그래프 이론, 그래프 탐색, 구현

제출 일자

2024년 7월 24일 02:11:22

문제 설명

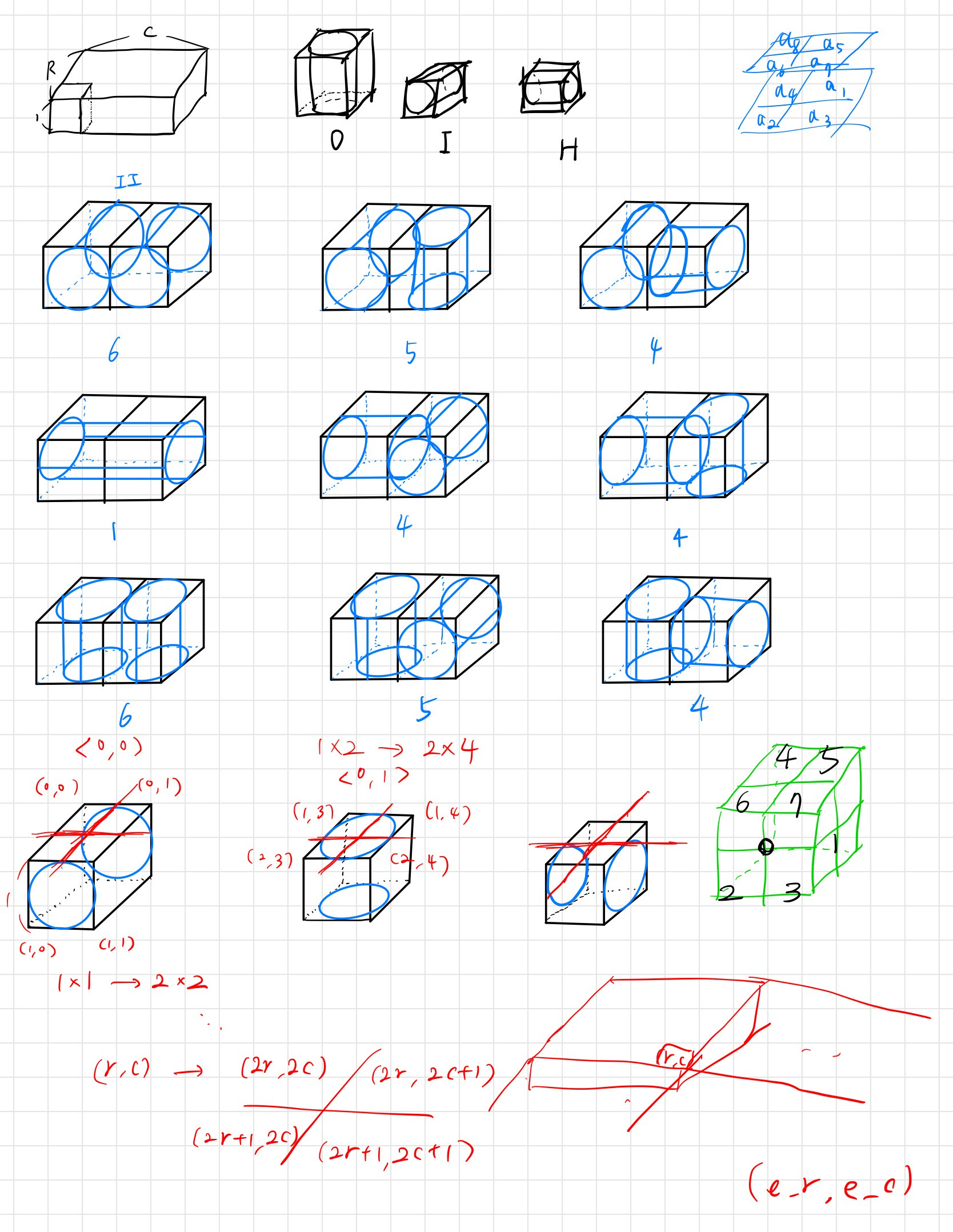
현우는 틀에 석고를 붓고 굳혀서 다양한 모양을 만들어 보는 취미가 있다. 현우가 이번에 준비한 틀은 세로 길이가 R, 가로 길이가 C, 높이가 1인 직육면체 모양이다.

만들어진 모양이 단순하면 석고 모형을 만드는 재미가 떨어진다. 그래서 현우는 지름과 높이가 1인 원기둥을 R × C개 가져왔다. 현우는 원기둥을 모두 틀 안에 배치한 다음 빈 공간에 석고를 붓기로 했다.

원기둥을 틀에 배치할 때에는, 틀을 R × C개의 단위 정육면체로 나눈 뒤 각 단위 정육면체 안에 꼭 맞게 넣어야 한다. 원기둥을 배치할 수 있는 방향은 세 가지가 있는데, 회전축이 가로를 향하거나, 세로를 향하거나, 바닥에 수직이도록 놓을 수 있다.

현우가 원기둥을 모두 배치하고 나면 틀에 석고를 부어 굳힌 뒤 모든 원기둥을 제거할 것이다. 그러면 여러 개의 분리된 석고 조각이 만들어진다. 예를 들어, 세로 길이가 1이고 가로 길이가 2인 직육면체 틀에 두 원기둥을 회전축이 바닥에 수직이도록 배치한다면 총 6개의 석고 조각이 만들어진다.

한편, 위 예시에서 원기둥 하나의 회전축이 세로를 향하도록 배치를 바꾼다면 총 5개의 석고 조각이 만들어진다.

현우가 틀에 원기둥을 배치하는 방법이 주어졌을 때, 총 몇 개의 석고 조각이 만들어질지 구해 보자.

입력

첫째 줄에 틀의 세로 길이와 가로 길이를 나타내는 정수 R와 C가 공백을 사이에 두고 주어진다. (1 ≤ R, C ≤ 200)

다음 R개의 줄에 걸쳐 현우가 틀에 원기둥을 배치하는 방법이 주어진다. 각 줄에는 길이 C의 문자열이 주어지며, 문자열을 구성하는 문자의 의미는 아래와 같다.

• H: 회전축이 가로를 향하는 원기둥
• I: 회전축이 세로를 향하는 원기둥
• O: 회전축이 바닥에 수직인 원기둥

출력

첫 줄에 석고를 굳힌 뒤 원기둥을 모두 제거하면 만들어지는 석고 조각의 개수를 출력한다.

문제 풀이

코드

import java.io.*;
import java.util.*;

public class Main {
	static BufferedReader br;
	static BufferedWriter bw;
    static StringTokenizer st;
    static int[] parents = new int[320000];
    static int R, C, extended_R, extended_C, ans;
    static char[][] c = new char[200][201];
    public static void main(String[] args) throws IOException {
//      br = new BufferedReader(new InputStreamReader(System.in));
        br = new BufferedReader(new InputStreamReader(new FileInputStream("input.txt")));
        bw = new BufferedWriter(new OutputStreamWriter(System.out));
        st = new StringTokenizer(br.readLine());
        
        R = Integer.parseInt(st.nextToken());
        C = Integer.parseInt(st.nextToken());
    	extended_R = R * 2;
    	extended_C = C * 2;

        Arrays.fill(parents, -1);

        for (int i = 0; i < R; i++) {
            c[i] = br.readLine().toCharArray();
            for (int j = 0; j < C; j++) {
            	cylinder(i, j, c[i][j]);
                connect(i, j);
            }
        }

		/*
		 * 결과 계산 루트 노드 값이 음수인 것의 개수 셈
		 * 이 개수가 연결되지 않은 영역의 수
		 */        
        ans = 0;
        for (int i = 0; i < 8* R * C; i++) {
            if (parents[i] < 0) ans++;
        }
        
        bw.write(String.valueOf(ans));
        bw.flush();
        bw.close();
        br.close();
    }

    public static int find(int x) {
        if (parents[x] < 0) return x;
        return parents[x] = find(parents[x]);

//        return parents[x] < 0 ? x : (parents[x] = find(parents[x]));
    }

    public static boolean isDivided(int x, int y) {
        x = find(x);
        y = find(y);
        // 붙어있으면
        if (x == y) return false;
        // 나뉘어졌으면
        parents[x] += parents[y]; // 집합 합치기
        parents[y] = x; // y의 부모를 x로
        return true;
    }

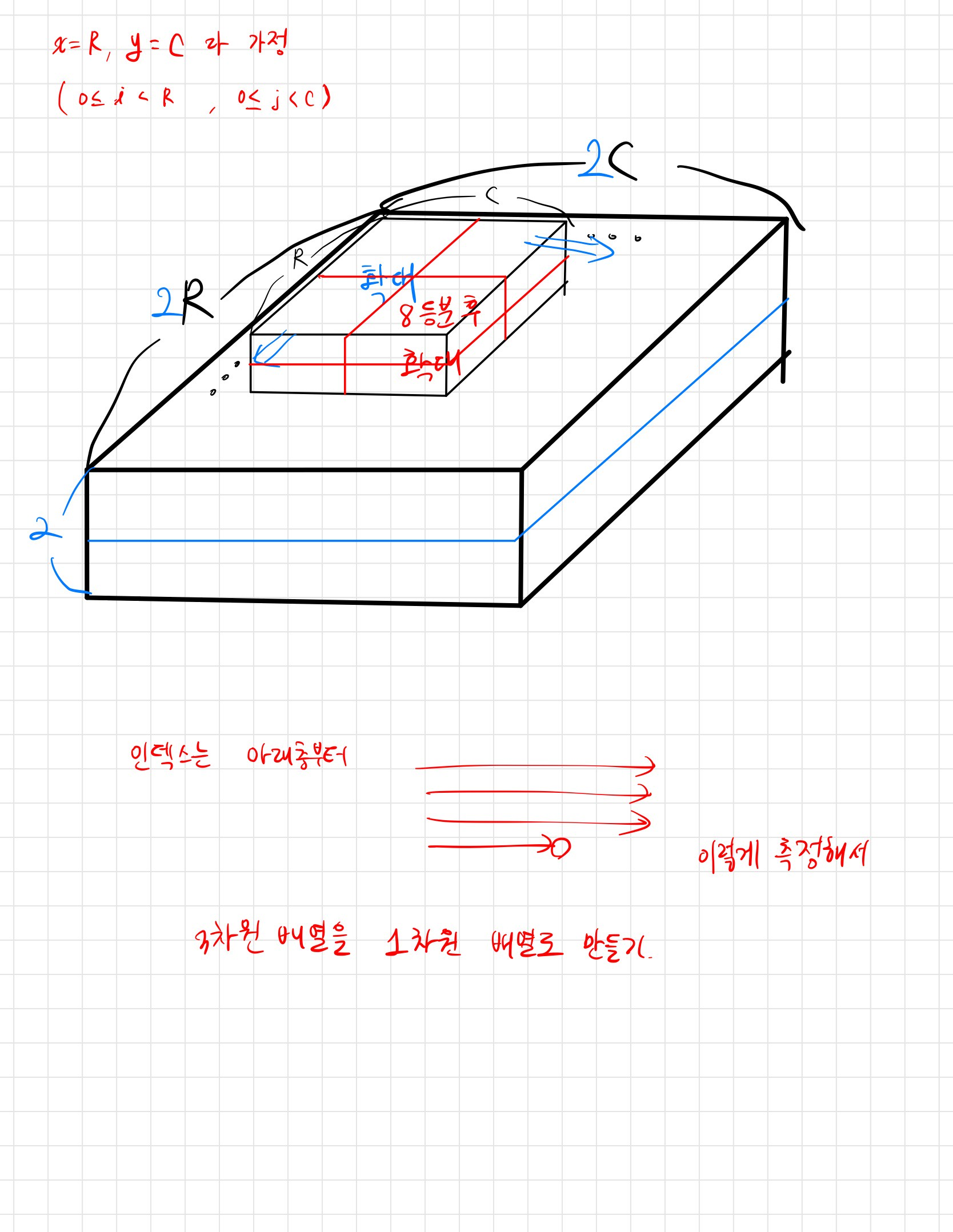
    public static void cylinder(int r, int c, char cylinder) {
    	/* 
    	 *  2x2 셀로 확장
    	 * (r, c) -> (2r, 2c), (2r, 2c+1), (2r+1, 2c), (2r+1, 2c+1)
    	 * (2r, 2c)     : a[0](1층) a[4](2층)
    	 * (2r, 2c+1)   : a[1](1층) a[5](2층)
    	 * (2r+1, 2c)   : a[2](1층) a[6](2층)
    	 * (2r+1, 2c+1) : a[3](1층) a[7](2층)
    	 * 
    	 */
        int doubled_r = r * 2, doubled_c = c * 2;
        int[] arr = new int[8];
        // 3차원을 1차원으로!
        // 2배 확대시킨 위치 인덱스 a[0] ~ a[3]
        arr[0] = doubled_r * extended_C + doubled_c;
        arr[1] = doubled_r * extended_C + doubled_c + 1;
        arr[2] = (doubled_r + 1) * extended_C + doubled_c;
        arr[3] = (doubled_r + 1) * extended_C + doubled_c + 1;
        
        // a[0] ~ a[3]가 2층에 위치한 형태
        for (int k = 4; k < 8; k++) arr[k] = arr[k - 4] + extended_R * extended_C;
        
        if (cylinder == 'O') {        	
        	isDivided(arr[0], arr[4]);
            isDivided(arr[1], arr[5]);
            isDivided(arr[2], arr[6]);
            isDivided(arr[3], arr[7]);
        }
        else if (cylinder == 'I') {
            isDivided(arr[0], arr[2]);
            isDivided(arr[1], arr[3]);
            isDivided(arr[4], arr[6]);
            isDivided(arr[5], arr[7]);
        }
        else if (cylinder == 'H') {
            isDivided(arr[0], arr[1]);
            isDivided(arr[2], arr[3]);
            isDivided(arr[4], arr[5]);
            isDivided(arr[6], arr[7]);
        }
    }

    public static void connect(int r, int c) {
        int doubled_r = r * 2, doubled_j = c * 2;
        int[] arr = new int[8];
        arr[0] = doubled_r * extended_C + doubled_j + 1;
        arr[1] = (doubled_r + 1) * extended_C + doubled_j + 1;
        arr[2] = (doubled_r + 1) * extended_C + doubled_j;
        arr[3] = (doubled_r + 1) * extended_C + doubled_j + 1;
        
        for (int k = 4; k < 8; k++) arr[k] = arr[k - 4] + extended_R * extended_C;
        
        for (int k = 0; k < 8; k++) {
        	// a[0], a[1], a[4], a[5]면서 마지막 열이 아닐때 가로로 연결
            if (k % 4 <= 1 && c + 1 < C) isDivided(arr[k], arr[k] + 1);
            
            // a[2], a[3], a[6], a[7]면서 마지막 행이 아닐때 세로로 연결
            if (k % 4 > 1 && r + 1 < R) isDivided(arr[k], arr[k] + extended_C);
        }
    }
}