BOJ_388354_홀짝트리 (Java)
[level 3] 홀짝트리 - 388354
성능 요약
메모리: 290 MB, 시간: 718.45 ms
구분
코딩테스트 연습 > 2025 프로그래머스 코드챌린지 1차 예선
채점결과
정확성: 100.0
합계: 100.0 / 100.0
제출 일자
2025년 03월 04일 16:35:14
문제 설명
루트 노드가 설정되지 않은 1개 이상의 트리가 있습니다. 즉, 포레스트가 있습니다.
모든 노드들은 서로 다른 번호를 가지고 있습니다.
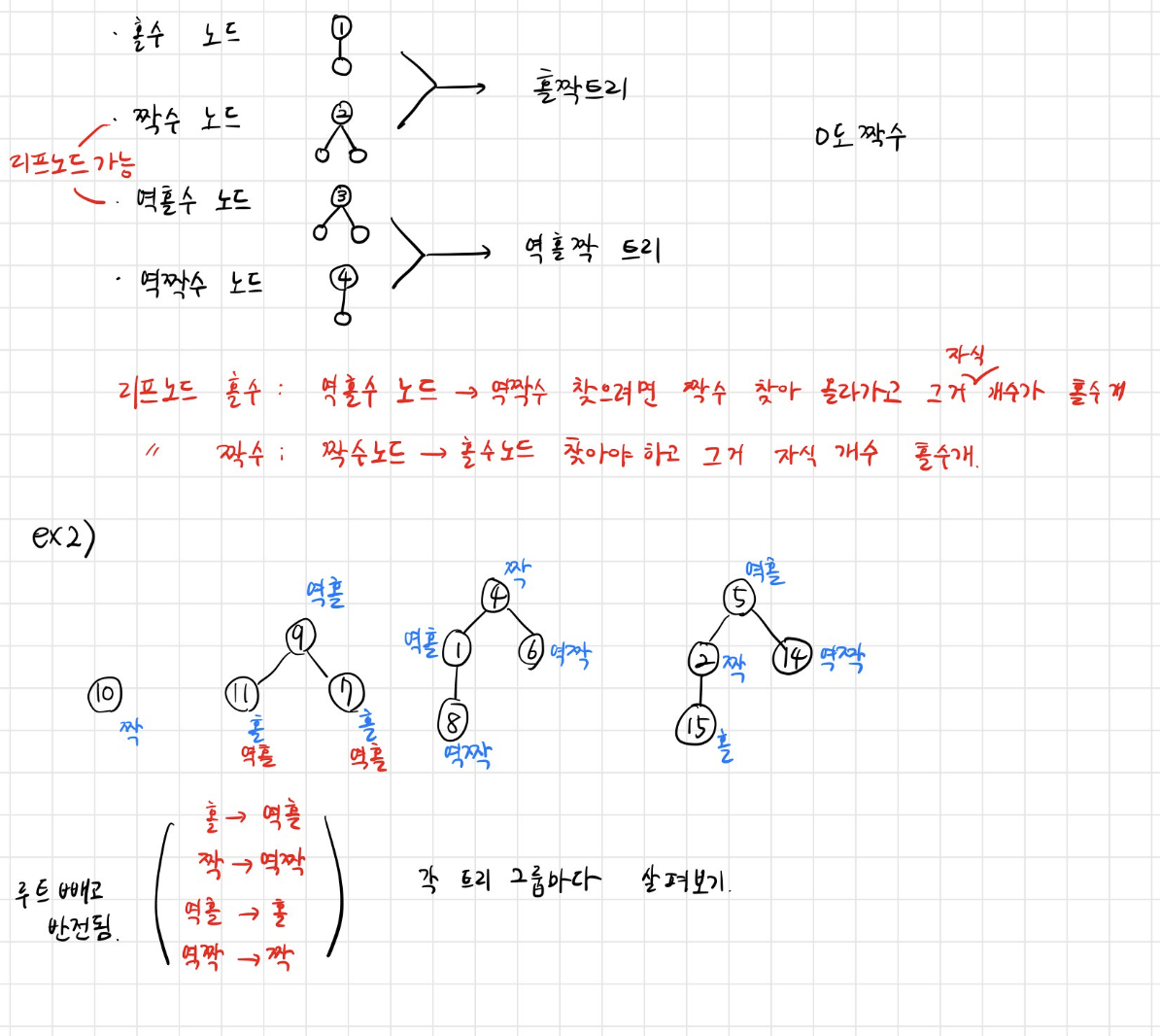
각 노드는 홀수 노드, 짝수 노드, 역홀수 노드, 역짝수 노드 중 하나입니다. 각 노드의 정의는 다음과 같으며, 0은 짝수입니다.
홀수 노드- 노드의 번호가 홀수이며 자식 노드의 개수가 홀수인 노드입니다.
짝수 노드- 노드의 번호가 짝수이며 자식 노드의 개수가 짝수인 노드입니다.
역홀수 노드- 노드의 번호가 홀수이며 자식 노드의 개수가 짝수인 노드입니다.
역짝수 노드- 노드의 번호가 짝수이며 자식 노드의 개수가 홀수인 노드입니다.
당신은 각 트리에 대해 루트 노드를 설정했을 때, 홀짝 트리가 될 수 있는 트리의 개수와 역홀짝 트리가 될 수 있는 트리의 개수를 구하려고 합니다. 각 트리의 정의는 다음과 같습니다.
홀짝 트리홀수 노드와짝수 노드로만 이루어진 트리입니다.
역홀짝 트리역홀수 노드와역짝수 노드로만 이루어진 트리입니다.
다음은 트리의 루트 노드를 설정하는 예시입니다.
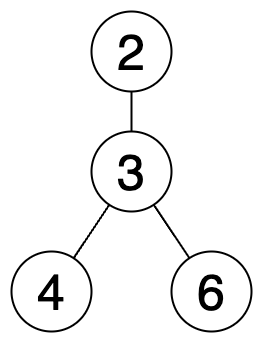
다음과 같은 트리가 있습니다.
위 트리의 루트 노드를 3번 노드로 설정하게 되면 다음과 같은 형태가 됩니다.
노란색 노드는 홀수 노드 혹은 짝수 노드를 나타내고, 빨간색 노드는 역홀수 노드 혹은 역짝수 노드를 나타냅니다. 이 경우, 모든 노드가 노란색이므로 홀짝 트리가 됩니다.
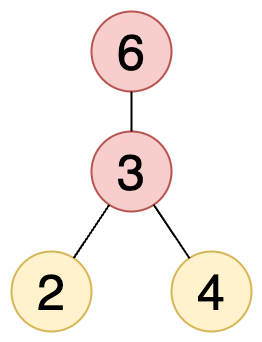
이 트리의 루트 노드를 6번 노드로 설정하게 되면 다음과 같은 형태가 되어 홀짝 트리 혹은 역홀짝 트리가 될 수 없습니다.
이와 마찬가지로 다른 노드를 루트 노드로 설정하는 경우에는 홀짝 트리 혹은 역홀짝 트리가 될 수 없습니다.
3번 노드를 루트 노드로 설정하는 경우에만 홀짝 트리가 될 수 있습니다. 따라서 위 트리는 홀짝 트리가 될 수 있는 트리입니다.
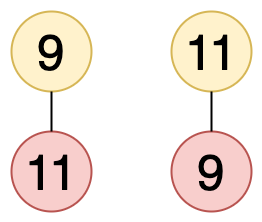
다음은 어떤 노드를 루트 노드로 설정하더라도 홀짝 트리 혹은 역홀짝 트리가 될 수 없는 트리입니다.
즉, 트리는 어떤 노드를 루트 노드로 설정하냐에 따라 홀짝 트리 혹은 역홀짝 트리가 될 수 있습니다. 경우에 따라 하나의 트리가 홀짝 트리와 역홀짝 트리 두 가지 모두 될 수 있거나 두 가지 모두 될 수 없을 수도 있습니다.
포레스트에 존재하는 노드들의 번호를 담은 1차원 정수 배열 nodes, 포레스트에 존재하는 간선들의 정보를 담은 2차원 정수 배열 edges가 매개변수로 주어집니다. 이때, 홀짝 트리가 될 수 있는 트리의 개수와 역홀짝 트리가 될 수 있는 트리의 개수를 1차원 정수 배열에 순서대로 담아 return 하도록 solution 함수를 완성해 주세요.
제한사항
- 1 ≤
nodes의 길이 ≤ 400,000- 1 ≤
nodes의 원소 ≤ 1,000,000 nodes의 원소는 중복되지 않습니다.
- 1 ≤
- 1 ≤
edges의 길이 ≤ 1,000,000edges의 원소는 [a,b] 형태의 1차원 정수 배열이며,a번 노드와b번 노드 사이에 무방향 간선이 존재한다는 것을 의미합니다.a,b는nodes에 존재하는 원소이며 서로 다릅니다.
- 포레스트인 경우만 입력으로 주어집니다.
테스트 케이스 구성 안내
아래는 테스트 케이스 구성을 나타냅니다. 각 그룹 내의 테스트 케이스를 모두 통과하면 해당 그룹에 할당된 점수를 획득할 수 있습니다.
| 그룹 | 총점 | 추가 제한 사항 |
|---|---|---|
| #1 | 10% | 하나의 트리만 주어집니다. nodes의 길이 ≤ 1,000, edges의 길이 ≤ 1,000 |
| #2 | 10% | nodes의 길이 ≤ 1,000, edges의 길이 ≤ 1,000 |
| #3 | 30% | 하나의 트리만 주어집니다. |
| #4 | 50% | 추가 제한 사항 없음 |
입출력 예
| nodes | edges | result |
|---|---|---|
| [11, 9, 3, 2, 4, 6] | [[9, 11], [2, 3], [6, 3], [3, 4]] | [1, 0] |
| [9, 15, 14, 7, 6, 1, 2, 4, 5, 11, 8, 10] | [[5, 14], [1, 4], [9, 11], [2, 15], [2, 5], [9, 7], [8, 1], [6, 4]] | [2, 1] |
입출력 예 설명
입출력 예 #1
문제의 예시와 같습니다.
홀짝 트리가 될 수 있는 트리가 하나 존재하고, 역홀짝 트리가 될 수 있는 트리는 존재하지 않습니다.
따라서 [1, 0]을 return 해야 합니다.
입출력 예 #2
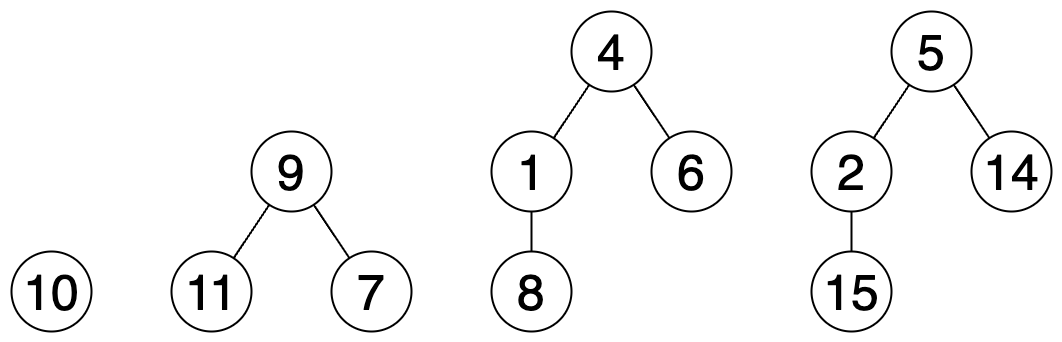
주어진 포레스트를 그림으로 나타내면 다음과 같습니다.
1, 3번째 트리는 각각 10번 노드, 4번 노드를 루트 노드로 설정하면 홀짝 트리가 될 수 있고, 2번째 트리는 9번 노드를 루트 노드로 설정하면 역홀짝 트리가 될 수 있습니다.
4번째 트리는 어떤 노드를 루트 노드로 설정해도 홀짝 트리 혹은 역홀짝 트리가 될 수 없습니다.
따라서 [2, 1]을 return 해야 합니다.
출처: 프로그래머스 코딩 테스트 연습, https://school.programmers.co.kr/learn/challenges
문제풀이
코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
import java.util.*;
class Solution {
static int[] p;
static ArrayList<Integer>[] board;
static Map<Integer, Integer> p_visited = new HashMap<>();
public int[] solution(int[] nodes, int[][] edges) {
/*
트리 그룹으로 나누고 각 그룹마다 홀짝트리 or 역홀짝트리 여부 보기
-> 홀짝이 1개면 g2++ , 역홀짝이 1개면 g1++
*/
int g1=0, g2=0; // g1 : 홀짝트리 수, g2 : 역홀짝트리 수
int s = 0;
for(int n : nodes){
if(s < n) s = n;
}
p = new int[s + 1];
for(int i=0; i<nodes.length; i++){
p[nodes[i]] = nodes[i];
}
board = new ArrayList[s+1];
for(int i=1; i< s + 1; i++){
board[i] = new ArrayList<>();
}
for(int[] e : edges){
board[e[0]].add(e[1]);
board[e[1]].add(e[0]);
}
for(int[] e : edges){
union(find(e[0]), find(e[1]));
}
for(int i=0; i<nodes.length; i++){
int node = find(nodes[i]);
if(!p_visited.containsKey(node)){
p_visited.put(node, 0);
int[] tmp = bfs(node);
if(tmp[0] == 1) g1++;
if (tmp[1] == 1) g2++;
}
}
int[] res = new int[]{g1, g2};
return res;
}
private void union(int x, int y){
int px = find(x);
int py = find(y);
if(px <= py) p[py] = px;
else p[px] = py;
return;
}
private int find(int x){
if(p[x] != x) return p[x] = find(p[x]);
return x;
}
private int[] bfs(int node){
int tmp_g1=0, tmp_g2=0; // 홀짝 and 역홀짝 개수세기
Queue<Integer> queue = new LinkedList<>();
Set<Integer> visited = new HashSet<>();
queue.offer(node);
visited.add(node);
while(!queue.isEmpty()){
int curr = queue.poll();
int currSize = board[curr].size();
if((curr + currSize) % 2 == 0) tmp_g1++;
else tmp_g2++;
for(int next : board[curr]){
if(visited.add(next)){
queue.offer(next);
}
}
}
return new int[]{tmp_g1, tmp_g2};
}
}