BOJ_6549_히스토그램에서 가장 큰 직사각형(Java)

[Platinum V] 히스토그램에서 가장 큰 직사각형 - 6549

문제 링크

성능 요약

메모리: 56948 KB, 시간: 968 ms

분류

자료 구조, 분할 정복, 세그먼트 트리, 스택

제출 일자

2024년 9월 30일 02:59:54

문제 설명

히스토그램은 직사각형 여러 개가 아래쪽으로 정렬되어 있는 도형이다. 각 직사각형은 같은 너비를 가지고 있지만, 높이는 서로 다를 수도 있다. 예를 들어, 왼쪽 그림은 높이가 2, 1, 4, 5, 1, 3, 3이고 너비가 1인 직사각형으로 이루어진 히스토그램이다.

히스토그램에서 가장 넓이가 큰 직사각형을 구하는 프로그램을 작성하시오.

입력

입력은 테스트 케이스 여러 개로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있고, 직사각형의 수 n이 가장 처음으로 주어진다. (1 ≤ n ≤ 100,000) 그 다음 n개의 정수 h₁, ..., h_n (0 ≤ h_i ≤ 1,000,000,000)가 주어진다. 이 숫자들은 히스토그램에 있는 직사각형의 높이이며, 왼쪽부터 오른쪽까지 순서대로 주어진다. 모든 직사각형의 너비는 1이고, 입력의 마지막 줄에는 0이 하나 주어진다.

출력

각 테스트 케이스에 대해서, 히스토그램에서 가장 넓이가 큰 직사각형의 넓이를 출력한다.

문제 풀이

1. 분할 정복

분할 정복 방식은 문제를 더 작은 부분으로 나누어 해결하는 방법입니다. 이 문제에서는 다음과 같이 적용됩니다:

1. 전체 히스토그램에서 가장 낮은 직사각형을 찾습니다.
2. 이 가장 낮은 직사각형을 기준으로 만들 수 있는 직사각형의 넓이를 계산합니다.
3. 가장 낮은 직사각형의 왼쪽 부분에 대해 1-2 과정을 반복합니다.
4. 가장 낮은 직사각형의 오른쪽 부분에 대해 1-2 과정을 반복합니다.
5. 2, 3, 4에서 구한 넓이 중 가장 큰 값을 선택합니다.

2. 세그먼트 트리

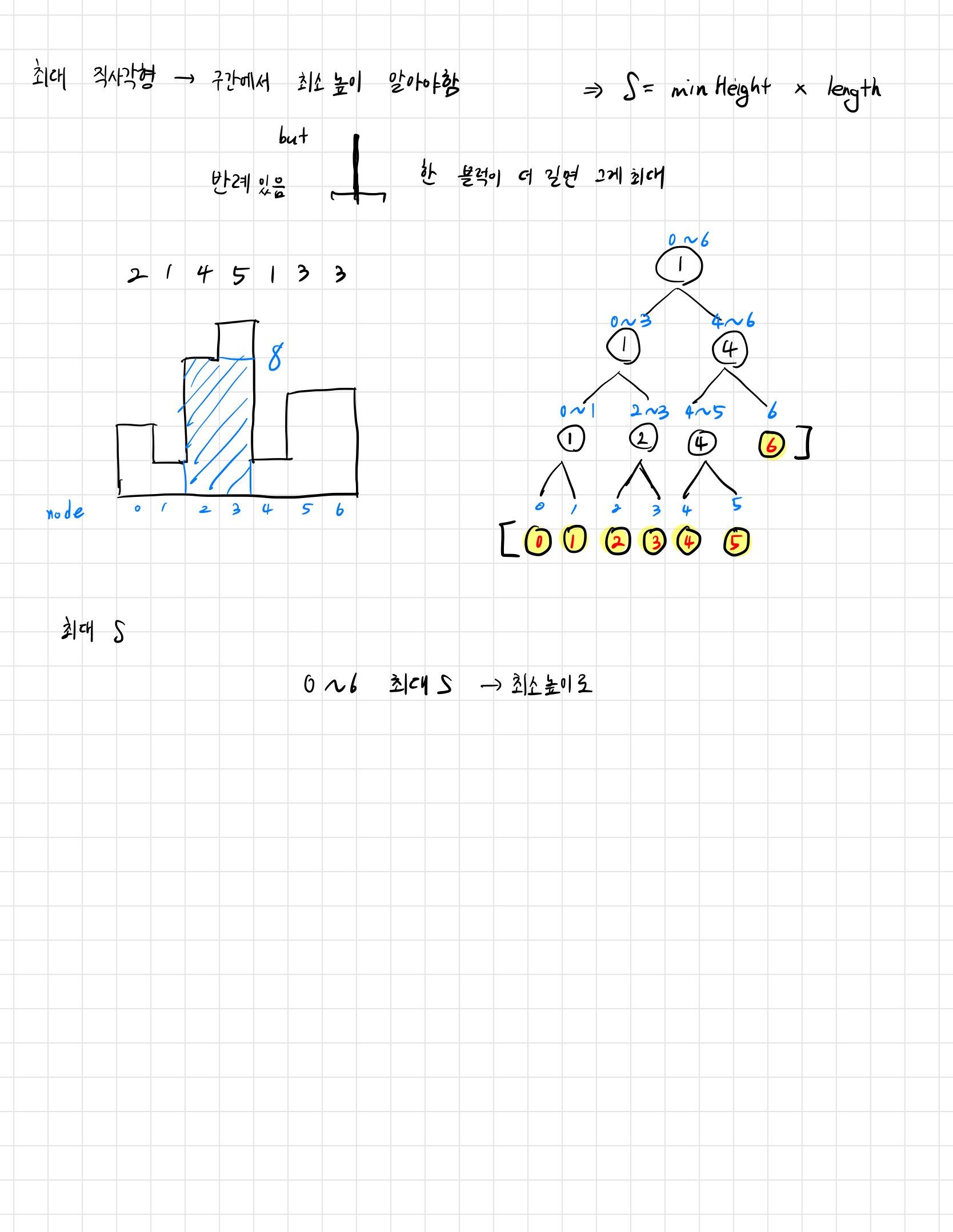
세그먼트 트리는 구간에 대한 정보를 빠르게 계산할 수 있게 해주는 자료구조입니다. 이 문제에서는 구간 내 최소 높이를 가진 직사각형의 인덱스를 빠르게 찾는 데 사용됩니다.

먼저 세그먼트 트리를 응용하는 것이 어려웠다. 기존 구간합, 구간 곱과 달리 넣는 값이 어려웠다. 각 구간에 최소높이를 넣으려 했는데 이후 모든 탐색을 통해 최소높이를 가져오긴 힘들었고, 결국 구간에서 최소 높이를 가진 블럭의 인덱스를 넣는 것으로 분할 정복을 가능하도록 만들었다.

그리고 최소 높이를 가진 좌 우를 탐색하였고 그럼 최대구간의 최소높이부터 좌우로 두 직사각형이 생기고 계속 나누며 최대 직사각형 넓이를 탐색했다. 시간복잡도는 O NlogN

코드

/**
 * Author: nowalex322, Kim HyeonJae
 */

import java.io.*;
import java.util.*;

public class Main {
	static BufferedReader br;
	static BufferedWriter bw;
	static StringTokenizer st;
	static StringBuilder sb;
	static int n, tree[], num[];
	
	public static void main(String[] args) throws Exception {
		new Main().solution();
	}

	public void solution() throws Exception {
//		br = new BufferedReader(new InputStreamReader(System.in));
		br = new BufferedReader(new InputStreamReader(new FileInputStream("input.txt")));
		bw = new BufferedWriter(new OutputStreamWriter(System.out));
		sb = new StringBuilder();
		
		while(true) {
			st = new StringTokenizer(br.readLine());
			n = Integer.parseInt(st.nextToken());
			if(n==0) break;
			
			num = new int[n+1];
			for(int i=1; i<=n; i++) {
				num[i] = Integer.parseInt(st.nextToken());
			}
			
			tree = new int[4*n];
			init(1, n, 1);
			
			long maxRecS = getMaxRectangle(1, n);
			sb.append(maxRecS).append("\n");
		}
		
        bw.write(sb.toString());

		bw.flush();
		bw.close();
		br.close();
	}

	/**
	 * a~b 까지 최대 직사각형 S 계산 후
	 * 좌우 분할정복으로 다시 계산 ( 다이아몬드 모양 )
	 * 
	 * @param left
	 * @param right
	 * @return
	 */
	private long getMaxRectangle(int left, int right) {
        if (left > right) return 0;

		long maxS = 0L;
		long tmpS = 0L;
		int idx = getMinH_idx(1, n, 1, left, right);
		
		maxS = (long)(right-left+1) * (long)num[idx];

		tmpS = getMaxRectangle(left, idx-1);
        maxS = Math.max(maxS, tmpS);
        
        tmpS = getMaxRectangle(idx+1, right);
        maxS = Math.max(maxS, tmpS);
        
		return maxS;
		
	}

	/**
	 * 주어진 구간에서 가장 낮은 직사각형의 인덱스
	 * 
	 * @param start
	 * @param end
	 * @param node
	 * @param left
	 * @param right
	 * @return
	 */
    private int getMinH_idx(int start, int end, int node, int left, int right) {
    	
        // 찾고자 하는 구간과 현재 노드의 구간이 겹치지 않으면 0 반환
    	if(left > end || right < start) return 0;
        
    	// 현재 노드의 구간이 찾고자 하는 구간에 완전히 포함되면 현재 노드의 값 반환
        if(left <= start && end <= right) return tree[node];
        
        
        // 그 외의 경우, 왼쪽 자식과 오른쪽 자식을 재귀적으로 탐색하여 더 낮은 높이를 가진 직사각형의 인덱스 반환
        int mid = (start + end) / 2;
        int leftIdx = getMinH_idx(start, mid, node*2, left, right);
        int rightIdx = getMinH_idx(mid+1, end, node*2+1, left, right);
        
        if(leftIdx == 0) return rightIdx;
        if(rightIdx == 0) return leftIdx;
        return num[leftIdx] < num[rightIdx] ? leftIdx : rightIdx;
    }

	/**
	 * 세그먼트 트리 초기화
	 * 최소 인덱스 저장
	 * 
	 * @param start
	 * @param end
	 * @param node
	 * @return
	 */
	private int init(int start, int end, int node) {
		if(start == end) return tree[node] = start;
		
		int mid = (start + end) / 2;
		int left = init(start, mid, node*2);
		int right = init(mid+1, end, node*2+1);
		
		return tree[node] = num[left] < num[right] ? left : right;
	}
	
}