PGMS_사칙연산 (Java)

[level 4] 사칙연산 - 1843

문제 링크

성능 요약

메모리: 52 MB, 시간: 0.96 ms

구분

코딩테스트 연습 > 동적계획법（Dynamic Programming）

채점결과

정확성: 55.6
효율성: 44.4
합계: 100.0 / 100.0

제출 일자

2024년 11월 12일 11:25:18

문제 설명

사칙연산에서 더하기(+)는 결합법칙이 성립하지만, 빼기(-)는 결합법칙이 성립하지 않습니다.
예를 들어 식 1 - 5 - 3은 연산 순서에 따라 다음과 같이 다른 결과를 가집니다.

• ((1 - 5) - 3) = -7
• (1 - (5 - 3)) = -1

위 예시와 같이 뺄셈은 연산 순서에 따라 그 결과가 바뀔 수 있습니다.
또 다른 예로 식 1 - 3 + 5 - 8은 연산 순서에 따라 다음과 같이 5가지 결과가 나옵니다.

• (((1 - 3) + 5) - 8) = -5
• ((1 - (3 + 5)) - 8) = -15
• (1 - ((3 + 5) - 8)) = 1
• (1 - (3 + (5 - 8))) = 1
• ((1 - 3) + (5 - 8)) = -5

위와 같이 서로 다른 연산 순서의 계산 결과는 [-15, -5, -5, 1, 1]이 되며, 이중 최댓값은 1입니다.
문자열 형태의 숫자와, 더하기 기호("+"), 뺄셈 기호("-")가 들어있는 배열 arr가 매개변수로 주어질 때, 서로 다른 연산순서의 계산 결과 중 최댓값을 return 하도록 solution 함수를 완성해 주세요.

제한 사항

• arr는 두 연산자 "+", "-" 와 숫자가 들어있는 배열이며, 길이는 3 이상 201 이하 입니다.
  • arr의 길이는 항상 홀수입니다.
  • arr에 들어있는 숫자의 개수는 2개 이상 101개 이하이며, 연산자의 개수는 (숫자의 개수) -1 입니다.
  • 숫자는 1 이상 1,000 이하의 자연수가 문자열 형태로 들어있습니다.. (ex : "456")
• 배열의 첫 번째 원소와 마지막 원소는 반드시 숫자이며, 숫자와 연산자가 항상 번갈아가며 들어있습니다.

---

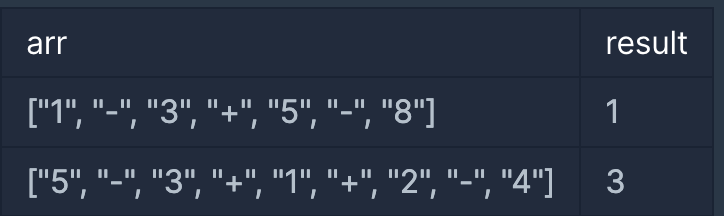
입출력 예

arr	result
["1", "-", "3", "+", "5", "-", "8"]	1
["5", "-", "3", "+", "1", "+", "2", "-", "4"]	3

입출력 예시

입출력 예 #1
위의 예시와 같이 (1-(3+(5-8))) = 1 입니다.

입출력 예 #2
(5-(3+((1+2)-4))) = 3 입니다.

출처: 프로그래머스 코딩 테스트 연습, https://school.programmers.co.kr/learn/challenges

코드

import java.util.*;

class Solution {
    static StringBuilder sb = new StringBuilder();
    List<String> divideInMinus = new ArrayList<>();
    public int solution(String arr[]) {
        for(String s : arr){
            if(s.equals("-")){
                if(sb.length()>0){
                    divideInMinus.add(sb.toString());
                    sb.setLength(0); // 새로운 객체 생성보다 부담 적고 delete연산은 이것보다 더 많은 연산 수행하므로 이게 제일 효율적
                }
            }
            else{
                sb.append(s);
            }
        }
        if(sb.length() > 0) divideInMinus.add(sb.toString());
    
        // 이제 뒤에서부터 덧셈으로 묶인 부분의 최솟값과 최댓값을 찾는다. 제일 첫번째 항목은 -가 불가능하므로 1번인덱스부터 끝인덱스를 역순으로.
        
        // 맨 앞 양수 항
        String[] firstNums = divideInMinus.get(0).split("\\+");
        int firstSum = 0;
        for(String num : firstNums){
            firstSum += Integer.parseInt(num);
        }
        
        int fromBackToSecond_Max = 0;
        int fromBackToSecond_Min = 0;
        
        for(int i=divideInMinus.size()-1; i>=1; i--){
            int currMax = calMax(divideInMinus.get(i));
            int currMin = calMin(divideInMinus.get(i));
            
            fromBackToSecond_Max = Math.max(currMax + fromBackToSecond_Max, currMin - fromBackToSecond_Min);
            fromBackToSecond_Min = Math.min(currMin + fromBackToSecond_Min, currMin - fromBackToSecond_Min);
        }
        
        int res = firstSum + fromBackToSecond_Max;
        return res;
    }
    private int calMax(String str){
        String[] nums = str.split("\\+"); // regex
        // String[] nums = str.split(Pattern.quote("+"));
        int max = (-1) * Integer.parseInt(nums[0]);
        for(int i=1; i<nums.length; i++){
            max += Integer.parseInt(nums[i]);
        }
        return max;
    }
    private int calMin(String str){
        String[] nums = str.split("\\+"); // regex
        // String[] nums = str.split(Pattern.quote("+"));
        int min = 0;
        for(String num : nums){
            min += Integer.parseInt(num);
        }
        return (-1) * min;
    }
}